|
Édition du: 01/04/2025 |
|
INDEX |
Nombres composés |
||
|
Composés durs ou
stables |
|||
Faites un double-clic pour un retour en haut de page
![]()
|
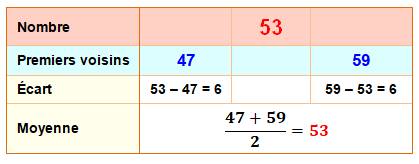
NOMBRES INTERPREMIERS Nombres tels que
ses deux premiers voisins sont à égale distance de lui-même. Exemple Le nombre 129 est à deux
unités de 127 et 131, ses deux plus proches nombres premiers. Le nombre 129 cumule cette propriété avec son carré, son cube et son
bicarré.
|
||
|
|
Sommaire de cette page >>> Nombres interpremiers >>> Liste des nombres interpremiers >>> Nombres 2-Interpremiers >>> Nombres 4-Interpremiers >>> Nombres Multi-Interpremiers |
Débutants Glossaire |
|
Définitions équivalentes Nombre composé ou premier
situé à égale distance des deux nombres premiers voisins. Triplet de trois nombres, le nombre et ses deux
nombres premiers voisins, en progression
arithmétique. Nombre égal à la moyenne
arithmétique de ses deux nombres premiers voisins |
Exemple
Le nombre
53 est premier et interpremier. Il s'agit d'un nombre premier
équilibré. |
|
|
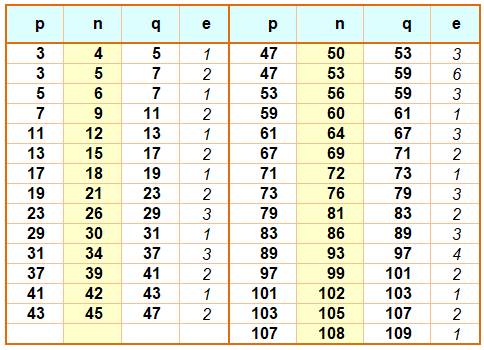
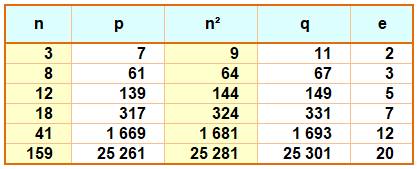
Table jusqu'à 108 On sélectionne les deux nombres premiers p et q,
l'un juste avant n et l'autre juste après n. Si l'écart avec le nombre n est identique, le
nombre est placé dans le tableau. Il est interpremier. La colonne e indique l'écart absolu entre n et ses voisins premiers. |
Exemple
|
|
|
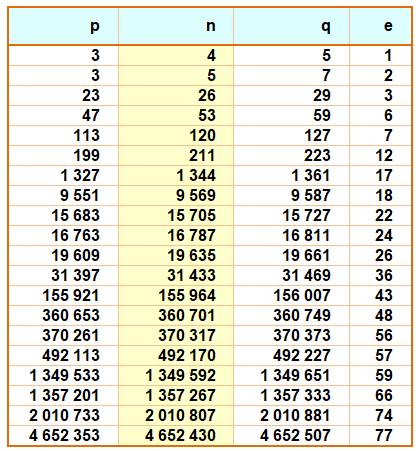
Liste jusqu'à 1000 En rouge, les nombres premiers
interpremiers que l'on nomme nombres premiers
équilibrés. |
4, 5, 6, 9, 12, 15, 18, 21, 26, 30, 34,
39, 42, 45, 50, 53, 56, 60, 64, 69, 72, 76,
81, 86, 93, 99, 102, 105, 108, 111, 120, 129, 134, 138, 144, 150, 154, 157, 160, 165, 170, 173,
176, 180, 186, 192, 195, 198, 205, 211, 217,
225, 228, 231, 236, 240, 246, 254, 257, 260, 263, 266, 270, 274, 279, 282, 288, 300, 309, 312,
315, 324, 334, 342, 348, 351, 356, 363, 370, 373,
376, 381, 386, 393, 399, 405, 414, 420, 426, 432, 436, 441, 446, 453, 459,
462, 465, 473, 483, 489, 495, 501, 506, 515, 522, 532, 544, 552, 560, 563, 566, 570, 574, 582, 590, 593, 596, 600, 604, 607, 610, 615, 618, 625, 636, 642, 645, 650, 653, 656, 660, 667, 675, 680, 687, 696, 705, 714,
723, 730, 733, 736, 741, 747, 754, 759, 765,
771, 780, 792, 803, 810, 816, 822, 825, 828, 834, 846, 855, 858, 861, 870,
879, 882, 885, 897, 909, 915, 924, 933, 939, 944, 947,
950, 960, 969, 974, 977, 980, 987, 994, … |
|
|
Records L'écart e sur une ligne est plus grand que tous les écarts
trouvés pour les nombres précédents. Compilation pour n jusqu'à dix millions. |
|
|
|
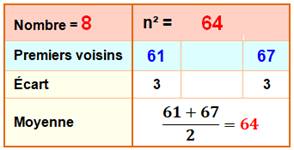
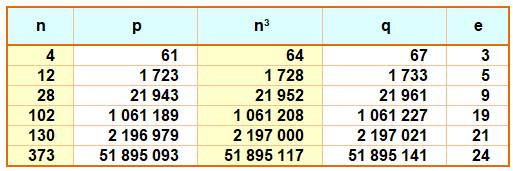
Définition Nombre tel que son carré
est interpremier. Exemple
|
Liste jusqu'à 1000 3, 8, 9, 12, 15, 18, 21, 25, 33, 41, 51, 60, 64, 72, 78, 92, 112, 117,
129, 138, 140, 159, 165, 168, 172, 192, 195, 198, 213, 216, 218, 228, 237,
273, 295, 298, 303, 304, 309, 322, 327, 330, 338, 342, 356, 360, 366, 387,
393, 408, 416, 429, 432, 441, 447, 456, 465, 473, 492, 508, 510, 513, 528,
534, 554, 560, 561, 567, 573, 580, 582, 588, 609, 626, 627, 642, 652, 666,
668, 678, 694, 708, 720, 726, 728, 735, 736, 744, 746, 756, 770, 786, 804,
806, 807, 818, 866, 868, 892, 897, 907, 948, 965, 975, 985, 996 Records
|
|
|
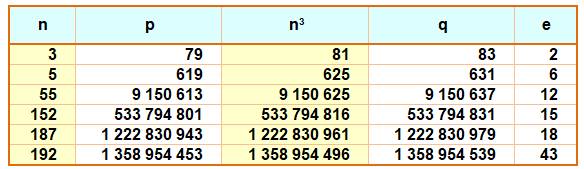
Définition Nombre tel que son cube
est interpremier. |
Liste jusqu'à 1000 4, 12, 16, 26, 28, 36, 48, 58, 66, 68, 74, 78, 102, 106, 112, 117,
124, 126, 129, 130, 148, 152, 170, 174, 184, 189, 190, 192, 224, 273, 280,
297, 321, 324, 369, 372, 373, 399, 408, 410, 421, 426, 429, 435, 447, 449,
450, 470, 475, 496, 504, 507, 531, 537, 549, 555, 561, 574, 576, 577, 595,
634, 644, 652, 680, 717, 729, 738, 756, 764, 766, 783, 805, 807, 810, 819, 834,
858, 867, 880, 882, 888, 894, 896, 900, 932 |
|
|
Records
|
||
|
Définition Nombre tel que son bicarré
est interpremier. |
Liste jusqu'à 1000 3, 5, 8, 21, 55, 66, 87, 99, 104, 105, 110, 120, 129, 135, 141, 144,
152, 168, 172, 186, 187, 192, 211, 222, 243, 279, 283, 295, 297, 321, 342,
385, 395, 398, 408, 425, 426, 460, 520, 541, 559, 597, 626, 627, 638, 642,
657, 666, 673, 680, 713, 755, 759, 765, 777, 783, 789, 795, 822, 858, 932,
940 |
|
|
Records
|
||
|
Interpremier ainsi que son carré.
|
9, 12, 15, 18, 21, 60, 64, 72, 129, 138, 165, 192, 195, 198, 228, 309,
342, 356, 393, 432, 441, 465, 473, 560, 582, 642, 736, 897 |
|
|
Interpremier ainsi que son cube.
|
4, 12, 26, 102, 129, 170, 192, 324, 373, 399, 426, 574, 680, 810, 834,
858, 882 |
|
|
Interpremier ainsi que son bicarré. |
5, 21, 99, 105, 120, 129, 144, 186, 192, 211, 279, 342, 426, 642, 680,
759, 765, 822, 858 |
|
|
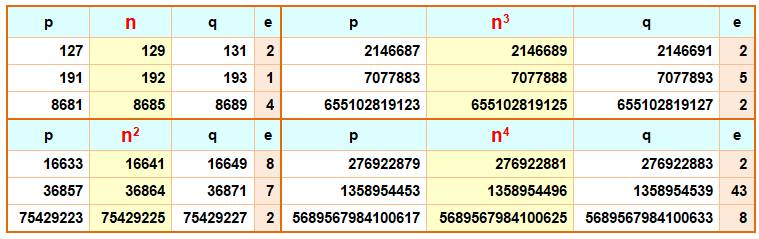
Interpremier ainsi que son carré et son cube. |
12, 129, 192, 1806, 1839, 6891, 8685, 8877 |
|
|
Carré, cube et bicarré sont interpremiers. |
129, 192, 408, 5250, 8535, 8685 |
|
|
Interpremier ainsi que son carré, son cube et son
bicarré. |
=> Détail en tableau ci-dessous |
|
|
|
||
Haut de page (ou
double-clic)
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |