Nombres premiers - écart à volonté

Édition du: 18/03/2021

M'écrire

Brèves de Maths

INDEX

Nombres premiers

Types de nombres

Classification

Nombres PREMIERS

Premiers

Intervalle

Écart à volonté

Orphelins

Intervalle – Tables

Puissances proches

Jumeaux

Écart entre nombres premiers

Suite de nombres composés

Il existe de nombreux couples de nombres premiers jumeaux (une infinité ?). Mais, à l'opposé, quelle est l'écart maximum entre deux nombres premiers successifs ? L'infini ! Oui, il est possible de trouver une suite infinie de nombres composés.

Exemple

Sommaire de cette page

>>> Suite de composés consécutifs

>>> Record d'intervalle entre nombres premiers

>>> Un million de nombres composés

>>> Exemples pour les premières suites

>>> Démonstration avec les FACTORIELLES

>>> Démonstration avec les PRIMORIELLES

Débutants

Nombres premiers

Glossaire

Nombres premiers

Nombres composés consécutifs – En bref

Pour tout n, on peut trouver n entiers consécutifs composés: il suffit de considérer les nombres (n + 1)! + k avec 1 < k < n.

Mais, il existe des suites bien avant d'atteindre (n + 1)! + 1.

Conjecture de D. Shanks: si p_n est le plus petit nombre premier qui suit n entiers composés, alors log p_n est proche de n. Le plus grand écart actuellement observé est 651. Il apparit pour les nombres 2 614 941 710, 599 et 2 614 941 711 251.

Cité par François le Lionnais- Publication de 1973

Wolf a émis une conjecture qui se rapproche un peu plus de l'observation:

Théorème de Dirichlet ou théorème de la progression arithmétique

Pour tous entiers naturels non nuls a et b premiers entre eux, il existe une infinité de nombres premiers de la forme a + n b, où n > 0.

Voir développments en Intervalle

Suite de composés consécutifs

Question

Est-il possible de trouver trente nombres composés qui se suivent ?

Réponse

Les nombres premiers sont fascinants, il y en a une infinité. De même, les nombres composés (non-premiers) sont étranges à leur façon. On peut en trouver autant que l'on veut qui se suivent. Donc, bien sûr, on peut en trouver trente ou trente mille.

Il y deux façons de justifier la réponse:

Une recherche systématique, ou

Une démonstration.

Recherche systématique

Cette première méthode assez sportive. Elle consiste à tester tous les nombres les uns après les autres. On peut utiliser une table des nombres premiers. Mais, évidemment un ordinateur, avec le bon programme, permet d'y arriver plus facilement.

Cette méthode présente un avantage important, elle donne la toute première séquence de 30 nombres composés.

On trouve ainsi la plus petite séquence de trente nombres composés consécutifs:

le premier des 30 est: 1 328

le dernier est 1 360

en fait, et en prime, il se trouve qu'il y en a 33.

La séquence que l'on trouve juste avant celle-ci en donne 21, et elle commence par 1 130. Ensuite, on passe directement à la suite des 33 indiquée.

Les premières séquences

Par exemple, la première séquence de 7 nombres composés successifs commence par 90 et se termine par 96.

1	3	5	7	13	17	19
1	8	24	90	114	524	888
	9	25	91	115	525	889
	10	26	92	116	526	890
		27	93	117	527	891
		28	94	118	528	892
			95	119	529	893
			96	120	530	894
				121	531	895
				122	532	896
				123	533	897
				124	534	898
				125	535	899
				126	536	900
					537	901
					538	902
					539	903
					540	904
						905
						906

Record d'intervalle entre nombres premiers

ou plus grande suite de nombres composés

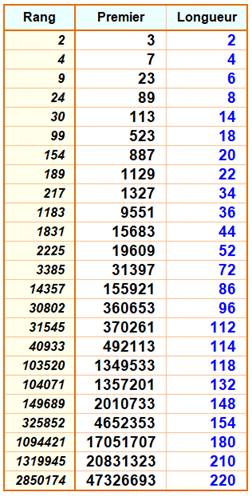
Record de longueur

L = P(n+1) – P(n)

Qté de nombres composés = L – 1

(En bleu, les valeurs explicitées

dans le tableau de droite)

1, 2, 4, 6, 8, 14, 18, 20, 22, 34, 36, 44, 52, 72, 86, 96, 112, 114, 118, 132, 148, 154, 180, 210, 220, 222, 234, 248, 250, 282, 288, 292, 320, 336, 354, 382, 384, 394, 456, 464, 468, 474, 486, 490, 500, 514, 516, 532, 534, 540, 582, 588, 602, 652, 674, 716, 766, 778, 804, 806, 906, 916, 924, 1132, 1184,, 1198, 1220, 1224, 1248, 1272, 1328, 1356, 1370, 1442, 1476, 1488, 1510, …

Record connu en 2020

1510 est la plus longue suite.

Rappel: on connait des suites bien plus longues, mais ici; il s'agit de la plus longue avec au départ le plus petit nombre premier.

Voir Références Internet pour valeur des nombres premiers

Un million de nombres composés

Question

Peut-on trouver une séquence de 1 million de nombres sans qu’un seul soit premier ?

Réponse

OUI ! C’est même possible pour une longueur quelconque ! Voire infinie …

Méthode avec les factorielles

On considère le nombre	1 000 001 !	Factorielle
Le premier nombre sera	1 000 001 ! + 2	Divisible par 2
Le suivant	1 000 001 ! + 3	Divisible par 3
	…
On continue	1 000 001 ! + i	Divisible par i
	…
Et pour finir par	1 000 001 ! + 1 000 001	Divisible par 1 000 001

Chacun des nombre formé par addition de i à factorielle un million est divisible par i. En effet, le nombre i , jusqu'à un million, est un des facteurs de 1 000 000! . Donc i divise cette factorielle, de même que la valeur i ajoutée; il divise la somme.

Soit un million de nombres premiers consécutifs non premiers.

On peut évidemment faire la même chose avec 1 000 001 ! – i

Ou avec toutes valeurs de n! et de i.

Voir Polynômes engendrant des composés

EXEMPLES pour les premières suites

On donne la table des nombres composés consécutifs obtenus par la méthode décrite ci-dessus.

On prend les valeurs successives de n de 2 à 10 et on explore n! + i avec i de 2 à n. En colonne de droite on explicite la divisibilité du nombre, montrant ainsi qu'il est composé.

n	i	c = n! + i	c/i
2	2	4	2
3	2	8	4
3	3	9	3
4	2	26	13
4	3	27	9
4	4	28	7
5	2	122	61
5	3	123	41
5	4	124	31
5	5	125	25
6	2	722	361
6	3	723	241
6	4	724	181
6	5	725	145
6	6	726	121
7	2	5042	2521
7	3	5043	1681
7	4	5044	1261
7	5	5045	1009
7	6	5046	841
7	7	5047	721
8	2	40322	20161
8	3	40323	13441
8	4	40324	10081
8	5	40325	8065
8	6	40326	6721
8	7	40327	5761
8	8	40328	5041
9	2	362882	181441
9	3	362883	120961
9	4	362884	90721
9	5	362885	72577
9	6	362886	60481
9	7	362887	51841
9	8	362888	45361
9	9	362889	40321
10	2	3628802	1814401
10	3	3628803	1209601
10	4	3628804	907201
10	5	3628805	725761
10	6	3628806	604801
10	7	3628807	518401
10	8	3628808	453601
10	9	3628809	403201
10	10	3628810	362881

Avec n = 10, on trouve, bien entendu, 9 nombres composés (non-premiers) de suite.

Il est clair que cette formule ne donne par forcément la première séquence de n nombres composés consécutifs.

Suite de composés consécutifs

Démonstration avec les FACTORIELLES

On se souvient des factorielles:

4! = 1 x 2 x 3 x 4 = 24

n! = 1 x 2 x 3 x 4 x … x n = n!

Voici une propriété qui va nous servir:

On ajoute un nombre à la factorielle:

3! + 2 = 1 x 2 x 3 + 2 = 6 + 2 = 8

et le résultat 8 est divisible par 2.

Normal 2 divise chaque terme de la somme 3! + 2;

Ceci est vrai pour tous les nombres de la factorielle.

n! + k = 1 x 2 x 3 x 4 x … x k x … n + k est divisible par k.

Suite de composés consécutifs

Démonstration avec les PRIMORIELLES

La primorielle d'un nombre est une factorielle particulière, ne comprenant que les nombres premiers successifs.

11!! = 2 x 3 x 5 x 7 x 11 = 2310

Il faut démontrer que N = n!! + i avec i de 2 à n est composé

Cas 1) – Si i est premier

Alors i divise n!! et aussi, i divise i;

Et, i divise la somme n!! + i ; N est composé.

Cas 2) – Si i n'est pas premier

Alors i est divisible par l'un de ses diviseurs premiers, disons: j .

Avec

Ce nouveau nombre premiers j, plus petit que n est l'un des facteurs de n!!, du fait de la définition de la primorielle.

Alors j divise n!! et aussi, j divise i;

Et, j divise la somme n!! + i ; N est composé.

Dans tous les cas,

N est un nombre composé.

Programme: écarts entre premiers

Calcul de la différence entre le (i + 1)^e nombre premier et le i^e du premier au centième.

Impression avec l'instruction spéciale d'impression à la suite (printf), assortie d'une demande de faire suivre le nombre d'une virgule et d'un espace.

Voir Programmation – Index

Retour	Nombres premiers – Index
Suite	Conjecture des premiers jumeaux Orphelins Infinité de premiers dans un intervalle donné Nombres composés Tables de facteurs Suite de nombres composés: 381, 3811 …
Voir	Calcul mental Curiosités de motifs et formes Géométrie Magie avec les nombres Théorie des nombres
Sites	Écart entre nombres premiers –Wikipédia OEIS A001223 – Prime gaps: differences between consecutive primes. OEIS A005250 - Record gaps between primes OEIS A111943 – Prime p with prime gap q - p of n-th record Cramer-Shanks-Granville ratio, where q is smallest prime larger than p and C-S-G ratio is (q-p)/(log p)^2. Shanks' Conjecture – Wolfram MathWorld Maximal Prime Gaps – Jens Kruse Andersen Prime gap – Wikipedia Table of Known Maximal Gaps – Chris K. Caldwell
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Premier/ecart.htm