NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 08/07/2023 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	Types de Nombres
Débutants Complexe	Nombres complexes			Glossaire Complexe
INDEX Complexes Types de Nombres	Introduction	Complexes	Quaternions	Octavions
	Historique	Factorisation	Trois Algèbres	Cyclotomique
		Sommaire de cette page >>> Approche >>> Définition des quaternions >>> Représentation >>> Rotations >>> Multiplication des quaternions >>> Propriétés >>> Norme >>> Intérêt

NOMBRES HYPERCOMPLEXES

QUATERNIONS

Généralisation du concept de nombres complexes

Nombres complexes: c = a + ib

Quaternions: q = a + ib + jc + kd

Octonions: 8 termes

APPROCHE

Les quaternions sont formés d'une quantité (un scalaire) et d'un vecteur (un point dans l'espace) soit 4 composantes au total. Durant de longues années, Hamilton (1805-1865)a cherché un nombre qui ne serait formé que de 3 composantes sans trouver une algèbre satisfaisante (les calculs ne collaient pas). Alors, il a eu l'idée d'ajouter une quatrième composante, et tout devenait bon! Avec une petite exception: pas de commutativité. Avec les quaternions l'ordre des termes importe. Plus tard, il a été démontré que 3 composantes n'est pas possible.

DÉFINITION des QUATERNIONS

Définition Quaternions: nombre complexe, formé de 4 composantes: q = a + ib + jc + kd  a, b, c et d sont des nombres réels; et i, j, k sont des coefficients imaginaires.  Propriétés des coefficients Les coefficients i, j, k sont tels que leurs produits donnent: i² = j² = k ² = i j k = – 1 ij = k = -ji jk = i = -kj ki = j = -ik Tableau de multiplication des coefficients entre eux (minuscules et majuscules par commodité, car non commutatif):

REPRÉSENTATION

ROTATIONS
Les rotations dans l'espace peuvent être décrites par les quaternions Formulation générale Avec q le quaternion adéquate pour effectuer la rotation désirée Exemples Rotation particulière Avec un angle 2q, alors q = cos q + (bi + cj + dk) sin q

MULTIPLICATION des QUATERNIONS
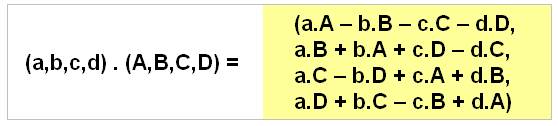
Exemples Notez la non commutativité D'une manière générale La multiplication est définie par:

PROPRIÉTÉS

Quaternions Structure de corps non commutatif, corps des quaternions de Hamilton, noté H. Un quaternion peut s'écrire: Q = C1 + j C2 où C1 et C2 sont des complexes (C = a + ib) Sur la même idée, existent les octavions de Cayley Le corps H des quaternions est Associatif Distributif NON Commutatif Conjugué q = a + ib + jc + kd q* = a – bi – cj – dk On peut vérifier que q q* = a² + b² + c² + d² = r Inverse q^-1 = (1 / qq*) . q*

NORME

Norme ou module des quaternions r = a² + b² + c² + d²  Le quaternion nul est le seul à avoir une norme nulle.  Norme du produit Le problème d'Hamilton dans ses recherches était de respecter la loi de multiplication: La norme du produit de 2 quaternions est égale au produit de leur norme. Cette loi était déjà connue d'Euler en 1705. Elle a été utilisée par Lagrange pour démontrer l'affirmation de Fermat disant que: tout nombre est la somme de 4 carrés.

INTÉRÊT
Mathématique pure:	Algèbres
Géométrie:	Rotation
Physique quantique:	Représentation du spin des particules

Suite	Octavions Quatrième dimension Nombres d'Hamilton Complexe – Index
Voir	Inventaire des types de nombres Nombre de Gauss Nombres – Glossaire et index Nombres réels
Site	Quaternionic Fractals par Andy Burbanks
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Type/ImagQuat.htm