|
||||||||||||||||||||||||||||||||||||||||
![]()
|
Partitions des nombres impairs Partitions des nombres impairs avec des nombres
impairs, consécutifs ou non. Propriétés et exemples. |
|
|
|||
|
Nombres consécutifs On sait
qu'un entier n est une somme de k nombres entiers consécutifs seulement si n
est divisible par k. Ex: (n-2) + (n-1) + n + (n+1) + (n+2) = 5n Avec n impair =
k . h, si h est impair alors n est la
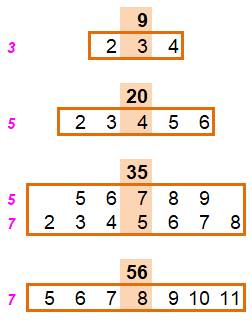
somme de k nombres consécutifs autour de h. Ex: 9 = 3 x 3, somme de trois consécutifs autour de
3. Avec n pair = k
. h, si h est pair alors n est la somme de
k nombres consécutifs autour de h. Ex: 20 = 5 x 4, somme de cinq consécutifs autour de
4. |
Exemples de sommes de consécutifs
|
||
|
Nombres en progression arithmétique Lorsqu'un
nombre est somme de k nombres consécutifs, il l'est aussi de k nombres en progression
arithmétique autour du même nombre (10 pour l'exemple). |
|
||
|
|
||
|
Un nombre impair ne peut être la
somme que d'une quantité impaire de nombres impairs. |
3 + 5 = 8 nombre
pair 3 + 5 + 7 = 15 nombre
impair (2k+1) + (2h+1) = 2(k
+ h + 1) pair (2k+1) +
(2h+1) + (2j+1) = 2(k + h + j) + 3 impair |
|
|
Théorème Seuls les nombres impairs divisibles par k sont sommes de k
impairs consécutifs; le nombre central est
égal au quotient. Seuls les nombres pairs
divisibles par k sont sommes de k pairs consécutifs;
le nombre central est égal au quotient. |
Exemple: 45 = 5 x
9: il est la somme de cinq nombres impairs consécutifs autour de 9: Exemple: 40 = 5 x
8: il est la somme de cinq nombres pairs consécutifs autour de 8: |
|
|
Exemple pour le nombre 45: toutes les partitions en sommes
d'impairs
|
||
|
|
||
|
Avec partitions impliquant des
nombres impairs quelconques, mais distincts, on a les premières partitions en
trois nombres impairs selon ce tableau: Il
y a seulement 16% des nombres impairs, non divisibles par 3, sommes de trois
impairs quelconques. En
revanche, la quantité de partitions pour chacun augmente rapidement. Ainsi 95
offre 44 telles partitions: 95 = 3+5+87 = 3+9+83 = 3+13+79 = 3+17+75 + … + 27+29+39
= 27+33+35. |
Les premières sommes
|
|
|
Liste des nombres impairs, non divisibles par 3, sommes de
trois impairs 19, 23, 31,
35, 43, 47, 55, 59, 67, 71, 79, 83, 91, 95, 103, 107, 115, 119, 127, 131,
139, 143, 151, 155, 163, 167, 175, 179, 187, 191, 199, 203, 211, 215, 223,
227, 235, 239, 247, 251, 259, 263, 271, 275, 283, 287, 295, 299, 307, 311,
319, 323, 331, 335, 343, 347, 355, 359, 367, 371, 379, 383, 391, 395, 403,
407, 415, 419, 427, 431, 439, 443, 451, 455, 463, 467, 475, 479, 487, 491,
499, … Ce sont
aussi les nombres égaux à 7
ou 11 mod 12
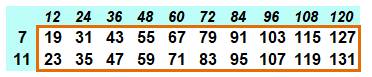
(sans 7 et 11). Sur le
tableau en haut, les multiples de 12; les deux lignes suivantes montrent
l'ajout de 7 ou 11. On y
retrouve les nombres de la liste ci-dessus.
19 = 12 + 7 et 23 = 12 + 11, etc. Théorème Tout
nombre égal à 7 ou 11 mod 12 est décomposable en sommes de trois nombres
impairs. Ce sont les seuls, à l'exception des nombres impairs divisibles par
3 qui, eux, sont sommes d'impairs consécutifs. |
||
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
|
|
|
Cette page |
![]()