|
Édition du: 01/09/2022 |
|
INDEX |
PARTITIONS sous contraintes |
||
Faites un double-clic pour un retour en haut de page
![]()
|
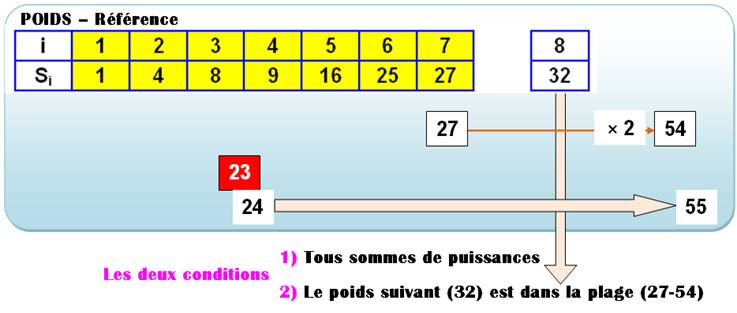
Partition sous contrainte de poids Théorème de Richert On se
donne une suite de nombres de référence
(poids). Quels sont les nombres atteints par la pesée avec ces poids uniques ? Quelles sont les conditions pour que
ces poids assurent la pesée de tous les nombres à partir d'un seuil ?
Exemple: la référence est la suite des puissances des
nombres (1, 4, 8, 9, 16 …). Le nombre 23 ne peut pas être somme de ces
puissances et c'est le seuil. En effet,
au-delà, tous les nombres sont somme de
puissances distinctes (un poids de référence est utilisé ou non, mais une
seule fois). Par exemple: 24 = 8 + 16.
|
||
|
|
Sommaire de cette page >>> Deux façons de voir les puissances >>> Approche du théorème de Richert >>> Première condition >>> Seconde condition >>> Théorème de Richert – Formulation >>> Résultats – Seuils (appli. Th. de Richert) |
Débutants Glossaire |
|
Théorème de
WARING |
Théorème de
RICHERT |
|
|
Concerne les nombres (a, b, …) à une puissance donnée (k): |
Concerne les nombres (a, b, …) à une puissance quelconque (k, h, …) ainsi qu'à toute sorte de
suites croissantes de nombres. |
|
|
n = ak
+ bk + …. |
n = ak
+ bh + …. |
|
|
239 = 1² + 2² + 3² + 15² |
32 = 1 + 4 + 27 = 1² + 2² +
33 |
|
|
Le
théorème de Waring indique qu'il existe un nombre-seuil (Wk) à
partir duquel tous les nombres sont une somme de nombres à la puissance k. |
Le
théorème de Richert indique qu'il existe un nombre-seuil (Rk) à
partir duquel tous les nombres sont une somme de nombres distincts pris dans
une suite donnée. |
|
Voir Théorème de
Waring
|
Une idée du théorème L'interprétation du théorème de Richert n'est pas
immédiate. Je tente une interprétation imagée avec l'exemple
du nombre 23, seuil à partir duquel tous les nombre sont somme de puissances
distinctes. Référence Cette formulation pour le nombre 23 figure dans le livre de David
Wells: Le dictionnaire Penguin des
nombres curieux (1995) – page 102. |
Nombre 23 Le nombre 23 n'est
pas somme de puissances parfaites*
distinctes. En effet, pour 22, on a: Seule possibilité pour aller plus loin, utiliser
le 16. Or, aucune somme avec 16 ne fait 23. * Sans la condition puissances parfaites, on
pourrait trouver: Conditions Ayant constaté que le nombre 23 semble être le seuil, alors, pour conclure que tous les nombres
au-delà sont somme de puissances distinctes, le théorème de Richert
demande à vérifier deux conditions. Conditions qui
s'appliquent à la plage de nombres allant du nombre seuil (23 + 1) au double
du dernier poids (2 x 27 + 1). |
|
|
Ici, on a choisi les sept premières puissances
comme références (poids). Puissance
parfaite incluant le 1.
|
||
|
Première condition On vérifie que tous les nombres de la plage (24-55)
sont somme de puissances distinctes, au moins une fois. |
Deuxième condition On vérifie que le poids suivant (32) est bien
dans la plage 27-54. Autrement-dit: toute nouvelle référence (32, 36 …) est inférieure
à deux fois celle qui précède (24, 32 …), et cela à partir d'un certain rang
k (ici, 7).
|
|
Voir Liste des puissances
parfaites successives
|
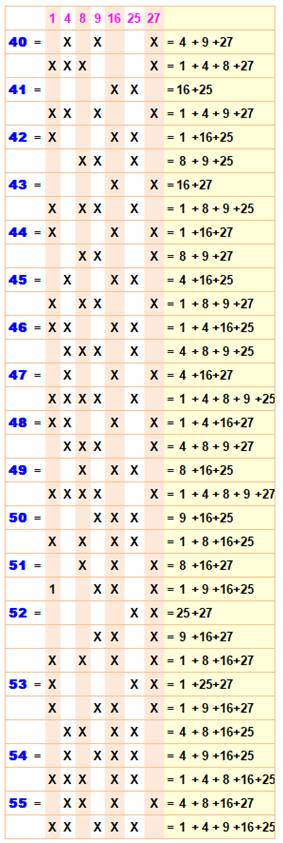
Ce qu'il faut vérifier Tous les nombres de la plage sont somme de
puissances distinctes. Présentation du tableau Le tableau présente cette vérification sous deux
formats: -
l'addition explicite. Bonus Pour information, on montre toutes les
présentations possibles. Ainsi, le nombre 25 a trois représentations en
sommes de puissances distinctes. Remarque Pour 32, ne soyez pas étonnés de ne pas retrouver
32 = 32 = 25. Normal, les poids utilisés s'arrêtent à 27. |
|
|
|
Vérification sur les premiers cas
En couleur, le cas examiné
ci-dessus: la nouvelle puissance 32 est bien comprise entre le précédent 27 et
son double 54. Le tableau montre que c'est bien vrai pour tous les cas listés
ensuite. Mais, ici, il faut montrer que c'est le cas
jusqu'à l'infini, même si cela parait évident. Une comparaison avec les
puissances de 2 fera l'affaire. |
||
|
Ce qu'il faut montrer
|
Démonstration
|
|
|
Énoncé et prouvé par H.-E. Richert
en 1949 Soit S = {s1, s2, …}, une
suite infini de nombres positifs croissants.
Alors, tout nombre n > N est somme d'éléments
distincts de S. |
L'enjeu est de trouver les valeurs de N et de k. La démonstration s'appuie sur le postulat
de Bertrand W. Sierpinski a généralisé le théorème à tout
type de suite. |
||
|
|
Formulation par Stefan Porubsky en 2009 – Czech Academy of Sciences, Prague |
||
|
6 |
Somme de
nombres premiers distincts. Every integer
n > 6 is the sum of distinct primes. |
|
|
9 |
Tout
nombre supérieur à 9 est la somme de nombres premiers impairs distincts. Every natural
number n > 9 is a sum of different odd prime numbers. |
|
|
11 |
Tout
nombre supérieur à 11 est la somme de deux ou plus nombres premiers
distincts. Every natural
number n > 11 is a sum of two or more different prime numbers. |
|
|
23 |
Tout
nombre supérieur à 23 est la somme de puissances distinctes. The largest
Integer not Sum of Distinct Perfect Power is 23. |
|
|
77 |
Le plus
grand nombre qui ne peut pas être une somme finie de nombres distincts plus
grands que 1 et dont la somme des inverses est 1. The greatest
integer that cannot be a finite sum of distinct integers greater than 1 whose
sum of their reciprocals is 1. |
|
|
1969 1349 1387 1475 |
Tout
nombre supérieur à 1969 est la somme de nombres premiers distincts de la
forme 12k + 1. (1349, 1387, 1475
respectivement pour 12k + 5, +7 et +11) Every natural
number n > 1969 is a sum of different prime numbers of the form 12k + 1.
(1349, 1387, 1475 respectively for 12k + 5, +7 et +11) |
|
|
La majorité de ces résultats sont énoncés dans le
livre: Elementatry Theory of Numbers by Sierpinsky – 1964 |
||
Voir
Anglais pour le bac et pour les affaires
Merci
à Hugo Selle pour
l'idée de cette page
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |