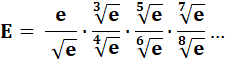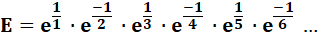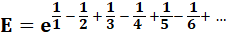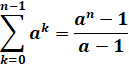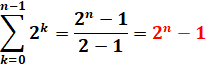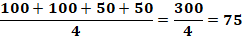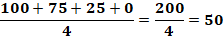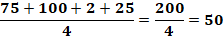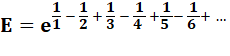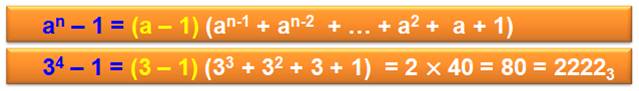NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 03/10/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Maths en se divertissant
Débutants Général	BRÈVES de MATHS									Glossaire Général
INDEX Brèves Atlas des maths	Page 1	Page 10		Page 20		Page 30		Page 40			Page 50
	Page 20 (380-399)		Page 21 (400-419)		Page 22 (420-439)		Page 23 (440-459)		Page 24 (460-479)
	Page 25 (480-499)		Page 26 (500-519)		Page 27 (520-539)		Page 28 (540-559)		Page 29 (560-579)

BRÈVES de MATHS – Page 21

Un millier de faits et chiffres

sur les nombres et les mathématiques

Ces pages sont dédiées à tous ceux qui veulent aborder les mathématiques en douceur et en s'amusant tout en découvrant les aspects les plus fondamentaux de cette discipline. Un parcours à picorer avec nombreux liens d'orientation vers les développements destinés à satisfaire votre curiosité.

En principe ces pages sont très abordables sans connaissances particulières de maths. Elles sont proposées dans un ordre quelconque favorisant la découverte de sujets multiples.

Anglais: Facts and figures about numbers and mathematics

400. Syllogismes
Énoncé classique Tout homme est mortel Socrate est un homme Socrate est mortel Aristote (Ou du moins prêté à Aristote)		Forme générique Tout B est A C est B Alors C est A Type Barbara Le type le plus classique		Illustration
Brèves associées	>>> Algorithmes		>>> Intelligence articicielle
Pour en savoir plus	>>> Les 14 types de syllogismes		>>> Carte postale 3224

401. Racine de 2 triple
Que vaut:		Formation d'un entier à partir de nombres irrationnels
Brèves associées	>>> Racine cubique jusqu'à deux chiffres		>>> Puissance de 2 – Échiquier >>> Carrés des nombres en 5
Pour en savoir plus	>>> Racines de 2 à étages >>> Nombres irrationnels		>>> Carte postale 3225

402. Sinus et cosinus & un DEMI
Partage de la tarte en six parts égales – Astuce Pour partager une tarte en six, je partage d'abord en 2 selon, disons, la ligne verticale de la figure. Je repère le milieu du rayon supérieur et mentalement, je dessine une horizontale qui coupe le bord de la tarte en un point que je note Je découpe selon un rayon qui aboutit à ce repère.
Brèves associées	>>> Valeurs trigonométriques		>>> Mesurer les angles >>> Lignes trigonométriques
Pour en savoir plus	>>> Le cas ½ en trigonométrie		>>> Trigonométrie >>> Terrain de jeu de la trigonométrie

403. Actualités 2018
Découverte d'un nouveau nombre premier, le plus grand avec 1,5 million de chiffres en plus du précédent record. Stephen Hawking (1942-2108): décès Robert Langlands: prix Abel
Brèves associées	>>> Conjecture Birch et Swinnerton-Dyer
Pour en savoir plus	>>> Actualités 2018	>>> Inventions

404. Nombres somme de carrés
Formulation mathématique et en anglais
Théorème des quatre carrés de Lagrange Un entier naturel m peut s'écrire comme la somme de quatre carrés (au plus) s'il est positif ou nul.			25 = 5² 26 = 5² + 1² 27 = 5² + 1² + 1² 28 = 5² + 1² + 1² + 1² 29 = 5² + 2²
Théorème des trois carrés de Fermat Ci-dessus, attribué à tord à Legendre, lequel caractérisera plutôt les résidus quadratiques. Tout entier naturel m peut s'écrire comme la somme de trois carrés s'il est positif ou nul et s'il n'est pas de la forme 4^a (8k + 7) avec a et k des entiers relatifs.			Somme de 3 carrés 25, 26, 27, 29, 30, 32, … Somme de 4 carrés 28, 31, 39, 47 …
Théorème de Fermat démontré par Euler Tout nombre premier supérieur à 2 peut s'écrire comme la somme de deux carrés si le reste de sa division par 4 est égale à 1 (p congru à 1 modulo 4).			11 = 2 x 4 + 3 NON 13 = 3 x 4 + 1 OUI et 13 = 3² + 2²
Brèves associées	>>> Somme des inverses des carrés >>> Calcul du carré des nombres à trois chiffres
Pour en savoir plus	>>> Théorème de Lagrange (4 carrés) >>> Théorème de Fermat (3 carrés)	>>> Théorème de Fermat (2 carrés)

405. Types de pseudo-premiers
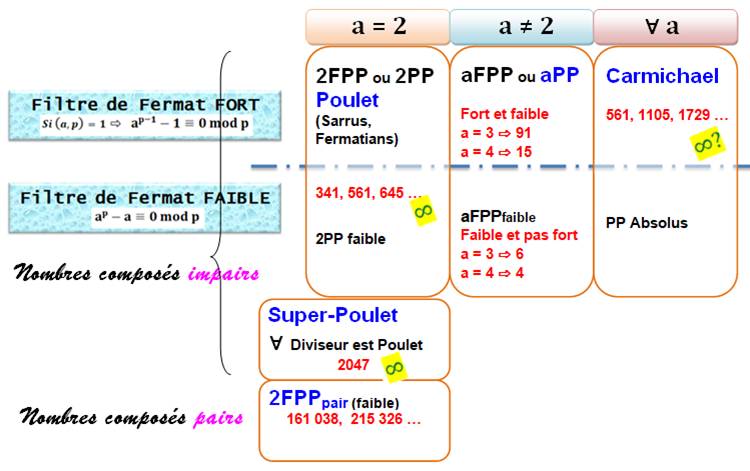
Deux critères pour classer les nombres pseudo-premiers de Fermat (FPP): La valeur de la base a & le type de condition de Fermat, forte ou faible Explications sur la page Primalité des nombres
Brèves associées	>>> Nombres pseudo-premiers – Introduction		>>> Petit théorème de Fermat
Pour en savoir plus	>>> Primalité des nombres	>>> Nombres pseudo-premiers >>> Nombres de Carmichael

406. Château et douves
Énigme Un jardinet est entouré d'eau. Vous désirez vous rendre au centre et vous ne disposez pas de cette planche de 5 m qui vous le permettrait. En revanche, vous avisez un tas de planches, mais toutes nettement plus courtes que 5 mètres. Réussirez-vous à rejoindre le jardinet ? Solution
Brèves associées	>>> Fortin et ses gardes		>>> Trois souris sur triangle
Pour en savoir plus	>>> Château et douves – Calculs		>>> Puits et les deux barres

407. Palintiples
Devinette Quel nombre de quatre chiffres se retourne lorsque multiplié par 4 ? What 4-digit number reverses its digits when multiplied by4 ? Palintiple Un palintiple est un nombre qui est égal à k fois son retourné avec k > 1. Le plus petit non trivial est 8712 dont le retourné 2178 vaut un quart de 8712.		Réponse 2178 x 4 = 8712 Quelques palintiples
Brèves associées	>>> Palindromes
Pour en savoir plus	>>> Palintiples		>>> Nombre 8 712

408. Nombres polis
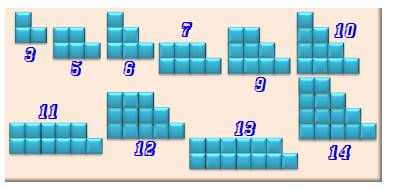
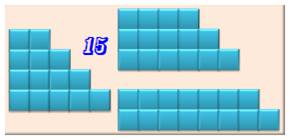
Définition Un nombre poli ou escalier est un nombre qui peut s'écrire sous la forme de une ou plusieurs sommes de deux ou plusieurs nombres consécutifs. Exemple: 15 = 1 + 2 + 3 + 4 + 5 = 4 + 5 + 6 = 7 + 8 Propriétés Les nombres polis ou en escaliers ou trapézoïdaux sont en fait tous les nombres entiers, sauf 1 et les puissances de 2. On calcule le degré de politesse d'un nombre un peu comme on calcule la quantité de diviseurs d'un nombre.		Nombres polis jusqu'à 14 Le nombre 15 est 3-poli
Brèves associées	>>> Nombres géométriques		>>> Nombres sandwiches
Pour en savoir plus	>>> Nombres polis – Introduction >>> Nombres polis – Développement		>>> Quantité de diviseurs

409. Nombres fluets (skinny numbers)
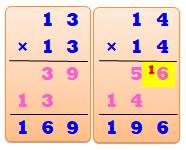
Un nombre fluet (skinny number) est un nombre sans création de retenue dans la multiplication par lui-même, c'est-à-dire, lorsqu'il est mis au carré. Le nombre 13 est fluet alors que 14 ne l'est pas du fait que dans la multiplication on trouve 4 x 4 = 16.
Un nombre fluet comporte: Jamais de 4; Un seul 3, mais alors sans 2; Des 2 mais alors sans 3; Un 2 ou deux 2, mais jamais trois 2; Des 0 et des 1 sans restrictions.		Nombres fluets jusqu'à 1000 1, 2, 3, 10, 11, 12, 13, 20, 21, 22, 30, 31, 100, 101, 102, 103, 110, 111, 112, 113, 120, 121, 122, 130, 200, 201, 202, 210, 211, 212, 220, 221, 300, 301, 310, 311, 1000.
Brèves associées	>>> Nombres auto-descriptifs		>>> Nombres de Harshad
Pour en savoir plus	>>> Nombre fluets		>>> Nombres à motifs

410. Hexagone magique
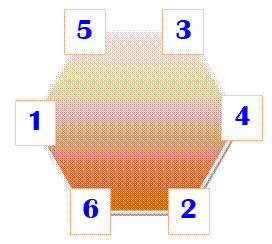
Énigme Énigme de niveau école primaire. Placez les nombres de 1 à 6 dans cet hexagone de sorte que la somme de deux nombres consécutifs soit toujours 6, 7 ou 8. Quelle est la valeur de x ? Note: le 1 est déjà placé, mais il pourrait être n'importe où.
Solution À partir du 1 déjà placé, pour atteindre 6, 7 ou 8, on a le choix entre 5 et 6 seulement. L'un va en haut du 5, l'autre en bas. Nombres qui restent: 2, 3 et 4. Après le 6, seul le 2 convient pour faire la somme 8; en effet, 3 et 4 sont trop grands. Avec le 3 et le 4 qui restent, seul le 4 convient après le 2. Soit deux solutions, dans un sens ou l'autre: [1, 5, 3, 4, 2, 6, 1] ou [1, 6, 2, 4, 3, 5, 1].
Brèves associées	>>> Séquence miroir		>>> Lapins et canards
Pour en savoir plus	>>> Hexagones magiques		>>> Carrés magiques – Index

411. Périmètre du rectangle divisé
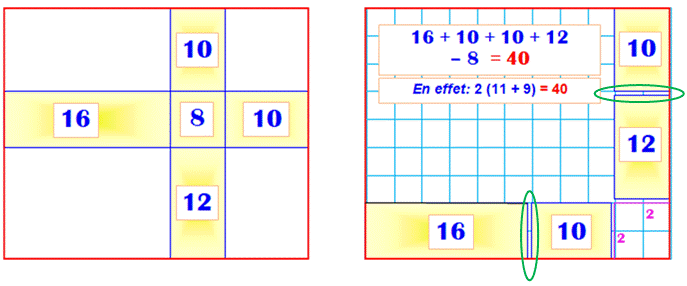
Énigme On donne la figure de gauche. Les nombres indiquent le périmètre des rectangles internes. Avec ces seules indications, retrouver le périmètre du grand rectangle.		Solution Plaquons les rectangles sur les bords comme sur la figure de droite. On observe que chaque côté des rectangles internes contribuent aux côtés du grand rectangle. Mais, les bords entourés de vert sont en trop ! Ils représentent le périmètre du rectangle central (ici, un carré) Bilan: il suffit alors d'ajouter le périmètre des rectangles internes et retrancher celui du rectangle central (ici un carré). Autre façon de voir Le périmètre de la croix est équivalent à celui du rectangle. C'est la somme des périmètres des rectangles moins celui du rectangle central.
Brèves associées	>>> Rectangle partagé		>>> Les neuf points en un seul trait
Pour en savoir plus	>>> Périmètre >>> Énigmes périmètres et aires		>>> Périmètre et autres énigmes

412. Égalité en 71 à rectifier
Rectifier cette égalité en ajoutant un seul point Solution
Brèves associées	>>> Dix en chiffres	>>> Nombre deviné ABC = k . A.B.C
Pour en savoir plus	>>> Nombre 71	>>> Jeux et énigmes – Index

413. Série avec exponentielle
Quelle est la valeur limite de E ?
Passons à l'écriture fractionnaire:
Produit à somme des exposants:
Avec la limite de cette suite
Brèves associées	>>> Suite de Sherlock Holmes		>>> Fraction et série infinie
Pour en savoir plus	>>> Série avec exponentielles		>>> Série harmonique

414. Nombres avec carrés
Première succession de quatre nombres avec facteurs carrés 242 = 2 x 11^2 243 = 3^2 x 3^3 = 3^5 244 = 2^2 x 61 245 = 5 x 7^2 Pour cinq 844 = 2^2 x 211 845 = 13^2 x 5 846 = 3^2 x 94 847 = 11^2 x 7 848 = 4^2 x 53		Liste des plus petites suites de k nombres avec des carrés [1, 4], [2, 8], [3, 48], [4, 242], [5, 844], [6, 22020] Les suivants dans l'ordre 217070, 1092747, 8870024, 221167422, 221167422, 47255689915, 82462576220, 1043460553364, 79180770078548, 3215226335143218, 23742453640900972, 125781000834058568, …
Brèves associées	>>> Nombres carrés		>>> Nombres sans facteurs carrés
Pour en savoir plus	>>> Nombres avec carrés – Records		>>> Nombres avec cubes – Records

415. Somme de puissances
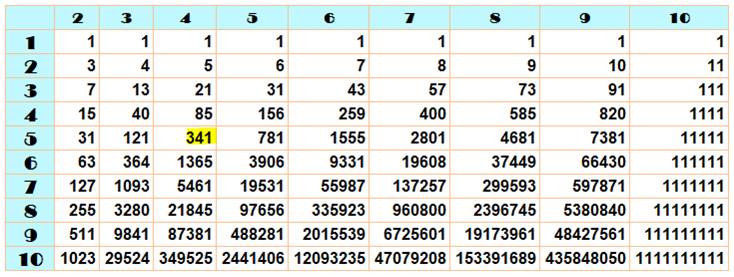
Formule générale Cas des puissances de 2		Exemples 4^0 + 4^1 + 4^2 + 4^3 + 4^4 = 1 + 4 + 16 + 64 + 256 = 341 = (4^5 – 1) / (4 – 1) – 1 = 1023 / 3 = 341 1 + 10 + 100 + 1 000 = 1 111 = (10^4 – 1) / (10 – 1) = 10 000 / 9 = 1 111 1 + 2 + 4 + 8 + 16 + …+ 1 024 = 2 048 – 1 = 2 047
Valeur de a en horizontal et de n en vertical Nombres de ce tableau jusqu'à 1111. Ils sont 37. 1, 3, 4, 5, 6, 7, 8, 9, 10, 11, 13, 15, 21, 31, 40, 43, 57, 63, 73, 85, 91, 111, 121, 127, 156, 255, 259, 341, 364, 400, 511, 585, 781, 820, 1023, 1093, 1111.
Brèves associées	>>> Carré = Somme de cubes		>>> Carré et cube à la fois
Pour en savoir plus	>>> Sommes à des puissances successives

416. Numération romaine médiévale
Numération curieuse utilisée au Moyen Âge. Elle mêle les chiffres romains classiques avec des multiples de 20 (système vigésimal). Elle est à l'origine de notre curieux quatre-vingts. L'illustration montre la notation classique des Romains (LXXX) pour le nombre 80. En bas, en bleu, les trois versions médiévales, la plus courante étant (IIIIXX) qui est la plus déroutante. Avec cette numération: IIIIXXX = IIII^XXX = 4 x 20 + 10 = 90 XIIIXXXIIII = XIII^XXXIIII = 13 x 20 + 14 = 274			Nombre 80 en chiffres romains
Brèves associées	>>> Chiffres romains	>>> Chiffres et nombres
Pour en savoir plus	>>> Numération romaine médiévale >>> Numération romaine	>>> Numération base 20 >>> Notre quatre-vingts – Pourquoi ? >>> Nombre 80

417. Carré magique des moyennes
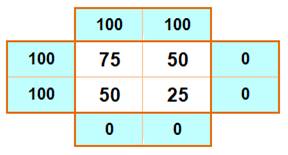
En bleu sur la périphérie du carré, les nombres indiqués sont des contraintes. Chaque nombre dans le carré central est la moyenne des quatre nombres qui l'entoure.		Généralisation à une grille d'ordre quelconque et à des contraintes (valeurs sur le pourtour) quelconques. Application à la propagation de la chaleur dans les matériaux.
Brèves associées	>>> Carré magique 3 x 3		>>> Carré magique à la demande
Pour en savoir plus	>>> Carré magique des moyennes		>>> Carrés magiques – Index

418. Triangle de Leibniz
Triangle formé à partir des nombres (fractions) de la série harmonique. Chaque ligne est constituée des inverses des termes du triangle de Pascal divisés par le numéro de la ligne (à partir de 1). Chaque terme est la somme des deux du dessous.
Brèves associées	>>> Triangle de Pascal		>>> Combinaisons de 7 parmi 15
Pour en savoir plus	>>> Triangle de Leibniz		>>> Série harmonique

419. Divisibilité de A^n – B^n
a^n – b^n est toujours divisible par (a – b) Ex: 7^n – 3^n divisible par 7 – 3 = 4 7^n – 6^n divisible par 7 – 6 = 1, et par 13 si n est pair. Cas où b = 1; où il est question de repdigits Le développement montre qu'un nombre à une puissance auquel on soustrait un, est un nombre composé; et, il s'écrit comme un repdigit dans la base puissance moins un. C'est un nombre brésilien.
Brèves associées	>>> Divisibilité des carrés et cubes	>>> Divisibilité du produit de nombres
Pour en savoir plus	>>> Divisibilité de A^n – B^n >>> Nombre brésilien	>>> Repdigit

Château et douves - Solution
Avec deux planches de 4,75 mètres, ça marche en les disposant comme indiqué. Retour

Rectifier cette égalité en ajoutant un seul point – Solution

Retour

Retour	Brèves de maths – Page 20
Suite	Brèves de maths – Page 22
Voir	Voir liens en haut de page
Cette page	http://villemin.gerard.free.fr/NombDico/aBreves/Breve21.htm