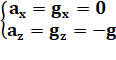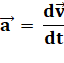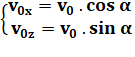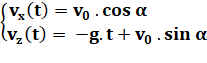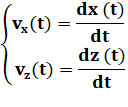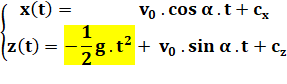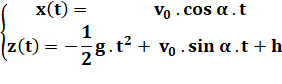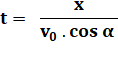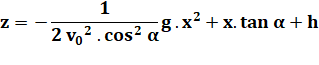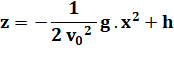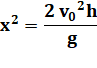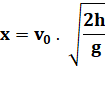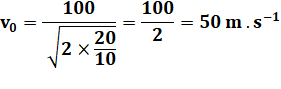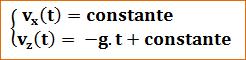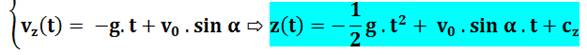|
|||||||||||||||||||||||||||||
![]()
|
Étude du mouvement du projectile Application des notions
apprises en terminale. Progressivement nous arriverons à déterminer le
mouvement du centre de gravité du projectile en déterminant l'accélération,
puis la vitesse, et finalement la trajectoire.
En fin de page, on trouvera des explications complémentaires pour les
non-aguerris, renvoyées par notes numérotées. |
|
Galilée démontre que pour des
projections effectuées avec le même impeto
selon des élévations différentes, la plus grande portée sera obtenue pour une
élévation de 45°;
toute projection effectuée sous un angle plus grand ou plus petit sera au
contraire plus courte. |
|
|
||||
|
|
|
|||
|
|
Direction Sens Valeur |
verticale vers le bas P
= m.g |
||
|
|
Direction Sens Valeur |
verticale vers le haut PA
= mA .g = |
||
|
Application numérique:
La poussée d'Archimède est de
très peu d'influence sur le mouvement du boulet. |
P
= PA
= = P/PA
= |
100 x 10 = 1000 N (100 kg de force) 1,3 x 30 x 10-3 x 10 0,39 N (39
g de force) 1000 / 0,39 = 2 564 |
||
|
|
Système Référentiel |
Le projectile Terrestre supposé galiléen |
|
|
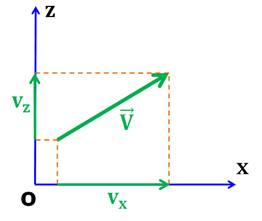
Poids & accélération |
|
|
(Composantes sur
les axes) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
la vitesse est constante
au cours du temps |
Le
mouvement en projection sur l'axe horizontal est uniforme. |
|
|
la vitesse varie au
cours du temps |
Le
mouvement en projection sur l'axe vertical n'est pas uniforme. |
|
Pour le centre de gravité G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Il
s'agit de l'équation de la parabole. La
trajectoire du boulet est donc parabolique. |
|
|
|
Le
mouvement du centre d'inertie G du projectile s'effectue dans le plan
vertical (z0x) contenant le vecteur vitesse Le
mouvement de la projection de g sur l'axe horizontal est uniforme et sur
l'axe vertical, il est uniformément varié. |
|
|
avec un tir horizontal |
|
|
|
|
z = 0 |
|
|
|
x = 100m h = 20 m |
Ce
qui correspond à 180 km/h |
Voir Calcul
pratique complet avec l'exemple d'un plongeur
(Tenant compte du temps de montée et
du temps de descente)
![]()
|
|
||
|
Note 1 Retour >>> |
Pourquoi noter le deuxième axe z plutôt que classiquement y en maths? Pour simplifier, nous travaillons dans le plan
vertical (deux axes x et z). En trois dimensions, il faudrait ajouter l'axe
de profondeur y. |
|
|
Note 2 Retour >>> |
Cet artifice est pratique car il permet de s'intéresser
séparement au mouvement du projectile selon chacun des axes. |
|
|
Note 3 Retour >>> |
Accélaration et relation
avec la vitesse: Il s'agit de décrire l'accélération en fonction du temps. Dans le cas général,
les coups d'accélation ou de déccélération modifient la valeur de la vitesse.
L'accélération à chaque instant montre comment se comporte la vitesse.
L'accélération est la dérivée
de la vitesse par rapport au temps. Connaissant la vitesse, passer à
l'accélaration consiste à dériver; connaissant l'accélération, passer à la
vitesse consiste à intégrer (calcul de primitive). |
|
|
Note 4 Retour
>>> |
Sur l'axe horizontal (x), l'accélération est nulle (le
poids n'agit pas dans cette direction). La primitive
est une constante. Sur l'axe vertical, l'accélération est celle de la
peanteur; celle qui fait tomber les objet sur le sol; celle qui est due au
fait que la Terre vous attire vers elle. Elle est égale à g. En fait, moins g
pour signifier que le sens est vers le bas. |
|
Note 5 Retour
>>> |
Comment s'y prendre pour touver la
primitive? Sur l'axe z, si l'accélération est constante
(ça continue à accéléer tout le temps!), la
|
|
Note 6 Retour
>>> |
Suite à la note 1, nous devons
exprimer les valeurs des projections sur les axes. Nous connaissons l'angle alpha du
vecteur avec l'horizontale. La partie sur l'axe x est en cosinus (cosinus à côté de
l'angle). La partie sur l'axe z est alors en sinus. |
|
Note 7 Retour
>>> |
Comment déterminer les constantes? Sur l'axe x, la vitesse est constante.
Or, nous savons qu'au temps initial (t = t0 = 0), la vitesse vaut:
v0 cos
Sur l'axe z, au temps initial la
vitesse est égale à une constante (car – g.t = 0). Or, nous avons qu'audépart
la vitesse vaut: v0 sin |
|
Note 8 Retour
>>> |
Nouvelle primitive à trouver pour
passer de la vitesse à la trajectoire. En x, la vitesse est constante, le
mouvement est une focntion linéaire du temps (à 100 km/h en voiture en deux heures, je parcours deux fois plus).
x en fonction du temps est égale à la vitesse multipliée par le temps, sans
oublier une constante toujours là dans les primitives.
En y, la vitesse est linéaire avec le
temps (- g.t), la primitive est d'un degré supérieur (2). La "recette" dans ce
cas est connue: la primitive de y = a . x est: Y = 1/2 ax² + cste (car la dérivée redonne
bien a.x). Appliquée ici, cela donne:
|
|
Cet
exemple est représentatif de tous les problèmes de chute ou de lancer de projectiles.
Il montre comment, à partir des lois de Newton et par intégrations
successives, il possible de déterminer la trajectoire d'un corps en
mouvement. Un
tel exercice sous cette forme ou voisine est souvent posée au baccalauréat. |
![]()
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
Calculateur |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/aScience/Physique/DYNAMIQ/Projecti.htm
|