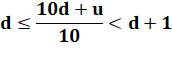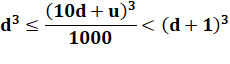NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 25/02/2021 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	EXPOSANTS
Débutants Général	PUISSANCES & RACINES								Glossaire Général
INDEX Puissance Analyse	Racine	Racine carrée			Racine de 2, 3 …			Racine treizième
	RACINE CUBIQUE (RC)
	Approximation			Calcul mental			RC de l'unité
	Calculs		Racine cubique à la main			Racines cubiques des complexes
			Sommaire de cette page >>> Nombres à 1 chiffre >>> Nombres à 2 chiffres >>> Nombres à 3 chiffres – Exemple 1 >>> Nombres à 3 chiffres – Exemple 2

RACINE CUBIQUE

Calcul mental

Comment calculer une racine cubique rapidement pour des nombres jusqu'à 1 milliard.

On donne un nombre au cube, retrouvez ce nombre.

Comme nous allons le constater, ce problème est relativement plus simple que le fait de calculer le cube. La méthode s'applique naturellement à d'autres types de racines.

Nombres à 1 chiffre
L'extraction de la racine cubique d'un nombre à n chiffre est particulièrement simple. D'abord, il s'agit d'un nombre inférieur à 1000 = 10^3. Comme tous les nombres en 4k – 1 Les chiffres des unités sont identiques sauf pour 2, 3, 7 et 8 pour lesquels c'est le complément à 10. Exemples de calcul de racine 216 = > chiffre des unités 6 => 216 = 6^3 512 = > chiffre des unités 2, complément à 10 = 8 => 512 = 8^3

Nombres à 2 chiffres
Méthode la plus simple On lit dans la table proposée, ou on apprend cette table par cœur. Unité: Comme pour un seul chiffre. 3 => 7 Dizaine: Prendre les milliers Lire le cube immédiatement inférieur dans la table. 50 => 27 => 3 La racine cubique de 50 653 est 37.
Pourquoi ça marche? Mettons le nombre de deux chiffres sous sa forme développée et calculons son cube. Les unités du cube sont celles de u^3	Quelle que soit la quantité de chiffres, les dizaines étant séparées (facteur 10), les unités du cube sont celles de u^3.
Pour les dizaines on procède par encadrement. On introduit d en ajoutant 10d partout. Puis division par 10. Avec le cube. Finalement en remarquant que 10d + u = n.	Les milliers d'un cube d'un nombre à deux chiffres est juste plus grand que ses dizaines.
Curiosité En utilisant cette mème technique de développement, on peut montrer que	Un nombre au cube diminué de ses unités au cube est divisible par 10 fois ses dizaines. Exemple 2345^3 – 5^3 = 12 895 213 500 12 895 213 500 / 2340 = 5 510 775

Autres méthodes sans table (pour information)

Selon la règle exprimée ci-dessus, le cas des unités est réglé; Reste à trouver les dizaines. Le plus grand est 99^3 = 970 299, disons inférieur à 1 million. Méthode 1 – Ordre de grandeur Cette méthode est facilitée par la connaissance des cubes des nombres de 1 à 9. Méthode 2 – Preuve par 11 La preuve par 11 permet de retrouver un chiffre manquant dans une opération. La racine numérique avec 11 est égale à la différence entre la somme des chiffres de rang impair et celle des chiffres de rang pair. On transpose l'égalité N = R^3 en égalité des racines numériques (monde du modulo 11). Trouvez un nombre au cube qui donne 0 en mod 11 n'est pas immédiat. On calcule la table une fois pour toute (les calculateurs prodiges la mémorise). Pour un cube égal à o, le tableau donne 0 et c'est la seule possibilité. On déduit la valeur de d le chiffre des dizaines.

Exemples méthode 1 1331 Unité: 1 Ordre de grandeur <20^3 = 8 000 Dizaine: 1 Racine cubique: 11 97 336 Unité: 6 Ordre de grandeur < 50^3 = 125 000 Dizaine: 4 Racine cubique: 46 704 969 Unité: 9 Ordre de grandeur < 90^3 = 729 000 Dizaine: 8 Racine cubique: 89 Exemples méthode 2 N = 166 375 R = sa racine cubique Unité de R: 5 RacN = (6+3+5) – (1+6+7) = 0 RacR = 5 – d RacN = RacR^3 0 = (5 – d)^3 (mod 11) 5 – d = 0 d = 5 Racine cubique: 55 N = 778 688 Unité: 2 RacN = (7+6+8) – (7+8+8) = – 2 = 11 – 2 = 9 mod 11 RacR = 2 – d RacN = RacR^3 9 = (2 – d)^3 (mod 11) 2 – d = 4 d = -2 = 11-2 = 9 mod 11 Racine cubique: 92 N = 19 683 Unité: 7 RacN = (1+6+3) – (9+8) = – 7 = 11 – 7 = 4 mod 11 RacR = 7 – d RacN = RacR^3 4 = (7 – d)^3 (mod 11) 7 – d = 5 d = 2 Racine cubique: 27

Suite pour trois chiffres

Pour trouver la racine cubique à trois chiffres, nous allons utiliser les méthodes employées ci-dessus:

Unité: selon la règle des unités,

Centaine: évaluée par la méthode de l'ordre de grandeur, et

Dizaine: par la méthode de la preuve par 11.

Nombres à 3 chiffres – Exemple 1
Cherchez la racine cubique de	N = R =	24 137 569
Ordre de grandeur	200^3 = 300^3 =	8 000 000 27 000 000
Quantité de chiffre de R Premier chiffre de N	R = c =	(3chiffres) 2
Unité	u =	9 (en effet 9^3 = 729)
Preuve par 9 La preuve par 9 n'est pas suffisante. C'est pourquoi elle n'est pas utilisée)	RacN = RacR = (11 + d)^3 = 11 + d = d =	1 2 + d + 9 = 11 + d 1 mod 9 1 ou 4 ou 7 mod 9 8 ou 2 ou 5
Preuve par 11 Les chiffres de rang impairs moins ceux de rang pair.	RacN = = RacR = RacR^3 = =	(4+3+5+9)– (2+1+7+6) 21 – 16 = 5 (c+u) – d = (2+9) – d (11 – d)^3 mod 11 5 mod 11
Recherche du chiffre central	(11 – d)^3 = 11 – d = d =	5 mod 11 3 (car 3x3x3 = 27 = 5 mod 11) 11 – 3 = 8
Bilan	R =	289

Nombres à 3 chiffres – Exemple 2
Cherchez la racine cubique de	N = R =	1 860 867
Ordre de grandeur	100^3 = 200^3 =	1 000 000 8 000 000
Quantité de chiffre de R Premier chiffre de N	R = c =	(3chiffres) 1
Unité	u =	10 – 7 = 3 (en effet 3^3 = 27)
Preuve par 11	RacN = = RacR = RacR^3 = =	(1+6+8+7)-(8+0+6) 22 – 14 = 8 (c+u) – d = (1+3) – d (4 – d)^3 mod 11 8 mod 11
Recherche du chiffre central	(4 – d)^3 = 4 – d = d =	8 mod 11 2 (car 2x2x2 = 8 mod 11) 4 – 2 = 2
Bilan	R =	123

Retour	Approximation d'une racine cubique
Suite	Racine de deux Racine de trois Calcul des racines carrées Calculs avec des racines cubiques Racine cubique à la main
Voir	Racines Nombres carré Puissances Constantes Cube Imaginaires Pi Nombre d'Or
Cette page	http://villemin.gerard.free.fr/Calcul/Puissanc/RacCube.htm