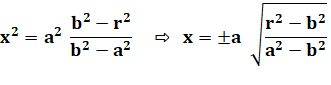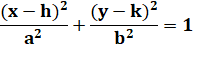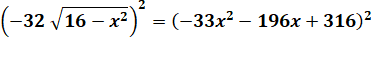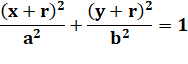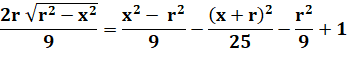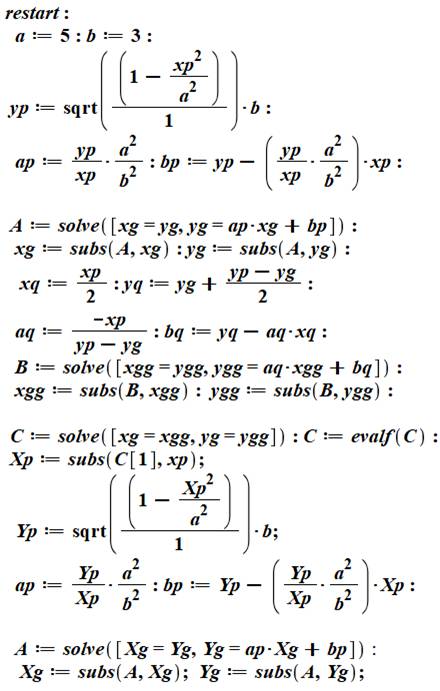|
Édition du: 18/08/2022 |
|
INDEX |
ELLIPSES |
|||
Faites un double-clic pour un retour en haut de page
![]()
|
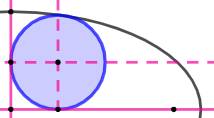
QUART d'Ellipse – Cercle inscrit
Une solution
graphique approchée est proposée. La solution
analytique conduit à résoudre des équations du quatrième degré et ne permet
pas de donner une formule simple du type r
= f(a, b) avec a et b, les demi-axes de l'ellipse. |
||
|
et plus |
Sommaire de cette page >>> Cercle et
ellipse >>>
Cercle et ellipse centrés >>>
Cercle avec ellipse décalée >>>
Quart d'ellipse – Tracé approché >>>
Résolution – Recherche du lieu du centre >>> Résolution
analytique par logiciel (Maple) >>>
Bilan |
Débutants Glossaire |
Humour
|
Pourquoi
les cercles n'invitent jamais les ellipses à leurs soirées ? Elles sont trop excentriques ! Why won't the circles invite the ellipses over for
diner ? They are too eccentric ! |
Voir Pensées et Humour
|
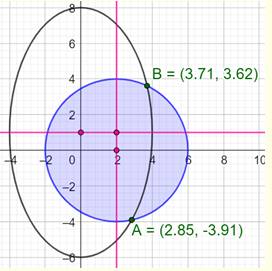
Intersections Selon leur position respectives et leur taille,
le cercle intersecte l'ellipse en 0, 1, 2, 3 ou 4 points. Détermination Calculer les coordonnées des points
d'intersection n'est simple que si:
|
|
|
|
Construction Une ellipse de demi-axes a = 5 et b = 3. Un cercle de même centre et de rayon 3,5. Les quatre points d'intersection A, B, C et D. Coordonnées des intersections
|
|
||
|
Équation du cercle et équation de l'ellipse |
|
||
|
Développement |
b²x²
+ a²r² – a²x² = a²b² x²
(b² – a²) = a² (b² – r²) |
||
|
Valeur de x Calcul identique pour y |
|
||
|
Cercle
Ellipse
|
|
||
|
Développement |
|
||
|
Application numérique |
(9 – 4) x² – 2 × 1
× 9x
+ (4 – 9) 4 + 1 × 9=0 5x²- 18x –11= 0 |
||
|
Dans ce cas, il est préférable de centrer les
axes sur l'un des objets; le plus simple, le cercle. Cercle centré Ellipse décentrée
|
|
||
|
Résolution numérique |
49x² + 196x + 16y² +32y – 572 = 0 |
||
|
Avec y² du cercle |
|
||
|
Radical isolé Puis carré Équation du quatrième degré Solution réelle Coordonnées recentrées |
-1089x4 – 12936x3 – 18584x2
+123872x – 83472 = 0 x1 = 2 + 0,85196… y1 = - 3,90821… |
||
|
Commentaires |
Calcul lourd ! Surtout sans logiciel. Le passage au carré génère de fausses solutions. De toute manière impossible de proposer une
formulation directe. Finalement, un tel calcul est déjà réalisé
par le logiciel GeoGebra,
alors pourquoi se priver. |
||
Alors le cercle inscrit
dans le quart d'ellipse ?
|
Avec l'ellipse, les choses ne sont jamais très
simples. La solution géométrique
n'existe pas (à ma connaissance). GeoGebra vient à notre secours pour une
solution aussi approchée qu'on le veut. La solution analytique
demande à connaitre les coordonnées des points d'intersection du cercle avec
l'ellipse. Nous venons de voir la difficulté du calcul. |
|
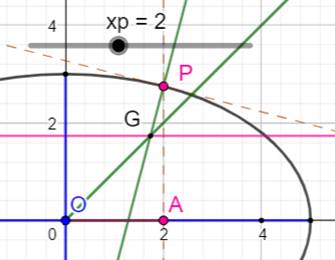
Construction Une ellipse de foyer F et F' avec a et b les
longueurs des demi-axes. Le cercle bleu inscrit dans le quart de
l'ellipse: tangent en P à l'ellipse et en A et B aux axes. Question Quel est le rayon r du cercle en fonction des longueurs
a et b des demi-axes ? |
|
|
|
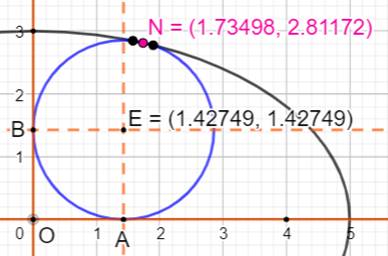
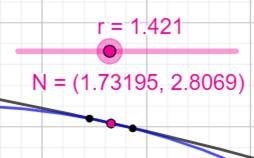
Expérience graphique Ellipse avec a = 5 et b = 3. Il n'existe pas de construction exacte avec la
règle et le compas (à ma connaissance). Avec GeoGebra, le cercle est mis en position
d'intersection de l'ellipse. N est le point milieu de la corde commune au
cercle et à l'ellipse. Le point de tangence est atteint si la longueur
de la corde est nulle. C'est-à-dire si les deux points noirs sont confondus
avec le point rouge. Le rayon du cercle est alors voisin de 1, 43. |
Approximation
|
|
|
Rappel Le logiciel GeoGebra est
très simple et gratuit. C'est le "Word" de la géométrie. Très utile
pour s'amuser. Précieux pour tester les solutions avant de les calculer; etc. Opérations Mettre un point aux quatre sommets de l'ellipse souhaitée. Mettre un curseur : outil curseur,
puis cliquer sur la zone de travail. Le dessin du curseur est affiché. Le
régler de 0 à 5 par exemple et le nommer r. Affiner la plage d'excursion du curseur: cliquer-droit sur le curseur
et sélectionner propriétés, puis introduire min, max et incrément de manière
à affiner la convergence. |
|
Exemples
|
|
Solution
analytique – Laborieuse ! |
|||
|
Données On raisonne avec une application numérique en
reprenant les données ci-dessus. On sera amené à conclure que la présence de
radicaux exclut la possibilité d'une belle formule pour r = (a, b). Démarche On raisonne à partir des équations de courbes en
prenant E comme origine des axes, ce qui simplifie l'équation du cercle et
permet de donner une valeur à y². |
Équation du cercle Il est centré sur le point E (0, 0) Équation de l'ellipse Elle est centrée sur O (-r, -r): |
||
|
Résolution de ces équations En remplaçant y par sa valeur dans l'équation de
l'ellipse. Une équation en x² = X avec présence sous un
radical. |
|
||
|
Isolation du radical et mise au carré pour le
supprimer. Conséquence, une équation du quatrième degré en
x. Je laisse
le soin au lecteur courageux de poursuivre ce calcul … |
Voir la démarche ci-dessus. |
||
|
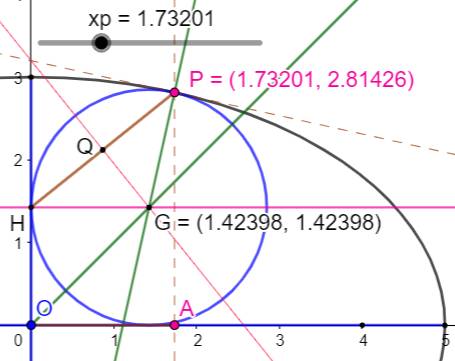
Construction On choisit OA =xp comme variable, l'abscisse du
point P sur l'ellipse Tangente en P et sa normale (verte). Bissectrice de l'angle entre les deux axes
(verte). Intersection G Le centre du cercle inscrit se trouve en G à
condition de bien choisir xp. En effet:
Depuis le point G, un perpendiculaire détermine le
point H. OH = HG correspond au rayon du cercle cherché. La dernière condition à remplir: GH = GP pour
assurer que le cercle passe par P. Le centre du cercle est donc sur la bissectrice
de HP. Il est aussi sur la tangente. Donc en G'. |
|
||
|
Bilan: il faut
ajuster xp pour que G et G' soient confondus. Avec cette méthode, il est aussi possible
d'ajuster le curseur xp pour arriver plus finement à la coïncidence. |
|
||
|
|
But Trouver les coordonnées du point P et la valeur
du rayon du cercle inscrit dans le quart d'ellipse. Commentaires La variable est xp. La valeur de yp est calculée
via l'équation de l'ellipse. La normale au point de tangence a pour équation y
= ax + b avec a = ap et b = bp. On cherche (A), l'égalité xg = yg sur cette
droite avec solve. L'instruction subs
permet d'extraire la valeur numérique de xg dans A, la solution de l'équation. Calcul des coordonnées (xq, yq) du point Q milieu
de HP. La médiatrice a pour équation y = ax + b avec a =
aq et b = bq. On cherche (B) l'égalité xgg = ygg sur cette
droite avec solve. Ayant les coordonnées de G (xg, yg) et de G'
(xgg, ygg), on cherche les conditions d'égalité avec solve
(C). Parmi toutes les solutions, on choisit la
première C[1].
On calcule les autres valeurs en reprenant les
équations du haut, mais avec, cette fois, une valeur numérique pour xp. Le programme imprime:
|
|
Voir Programmation – Index / Équation
de la droite
|
Recherche du rayon du cercle inscrit dans le quart de cercle:
|
![]()
|
Retour |
|
|
|
Suite |
|
|
|
Voir |
|
|
|
Sites Aucun
ne donne la solution au problème du
quart d'ellipse. |
|
|
|
Cette page |
http://villemin.gerard.free.fr/Geometri/Coniques/EllipseQ.htm |
|