|
||||||||||||||||||||||||||||||||
![]()
|
|
||
|
Nombre carré centré / nombre
triangulaire carré / Nombre carrément carré / Nombre
carré-carré / Nombre doublement carré |
||
|
Définitions |
NOMBRE CARRÉ
|
|
|
Formule |
Cn = n² |
|
|
Caracté-risation |
Si l'unité vaut 0, la dizaine vaut 0 aussi (cf. 10² = 100). Si l'unité vaut 5, la dizaine vaut 2 (cf. 5² = 25)
Voir Recherche d'un nombre
carré |
|
|
Génération |
|
|
|
Impairs |
Exemple:
6² = 36 = 1 + 3 + 5
+ 7 + 9 + 11 Illustration:
25 = 1 + 3 + 5 + 7 + 9 Voir Calcul de la racine carrée avec les
impairs |
|
Propriétés |
P. Erdös
et Rugge
Soit n est
premier et son carré est composé; soit il est composé, et chacun de ses
facteurs premiers est au carré, produisant un nombre composé.
Exemple: 7² = 6 x 8 + 1 = 48 + 1 = 49 Raison: (n +
1) (n – 1) = n² - 1
Exemple: 7² = 6² + 2 x 7 - 1 = 36 + 14 –
1 = 49 Raison: n² -
(n-1)² = n² - n² + 2n - 1 = 2n – 1
Exemple: 7² = 2 x 6² - 5² + 2 = 72 – 25 + 2 = 49 Raison: 2(n-1)² - (n-2)² + 2 = 2n² - 4n + 2 –
n² + 4n – 4 + 2 = n²
Exemple: 6² = 36 = 15 + 21
Exemple: 5² = 3² +
4²: 25 est impair et 5 = 1² + 2².
Exemple: 4 x 9 = 36 = 6² et 4 = 2² comme 9 = 3².
Exemple: 15² = 225 = 9 x 25 et 3 divise 15, comme
5 divise 15. |
|
|
Imaginaire |
|
|
|
Anglais |
|
|
|
|||||
|
|
|||||
|
Le carré d'un nombre à n chiffres aura 2n – 1 ou
2n chiffres (11² = 121, … 31² = 961, 32² = 1024,
… et 99² = 9801). Les nombres à partir desquels le carré prend un
chiffre de plus, pour n avec le même nombre de chiffres : [32, 1024], [317, 100489], suite ci-dessous. Ce sont les plus petits carrés à 2k chiffres. Un carré à n chiffres est le carré d'un nombre à
n/2 chiffres si n est pair et 1/2 (n + 1) chiffres si n est impair. |
Plus petits carrés à 2k chiffres

Carrés avec minimum de chiffres
|
Carrés avec seulement deux chiffres différents de n = 10 à 10
000, hors nombres en 10, comme 10² = 100 [11,
121], [12, 144], [15, 225], [21, 441], [22, 484], [26, 676], [38, 1444], [88,
7744], [109, 11881], [173, 29929], [212, 44944], [235, 55225], [264, 69696],
[3114, 9696996] Aucun
carré avec un seul chiffre |
Voir Carrés
avec chiffres répétés
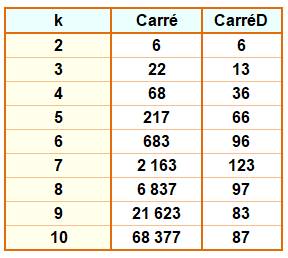
Quantité
de carrés à k chiffres dont carré à chiffres distincts
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()




