|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
PARTITIONS – Quantité Formule de récurrence Calcul de la quantité de
partitions à partir d'une formule de récurrence. On nomme p(n, k), les partitions
du nombre n avec les seulement les nombres de 1 à k. Il s'agit bien de partitions (sans compter les permutations des
nombres). |
|
|
|||
|
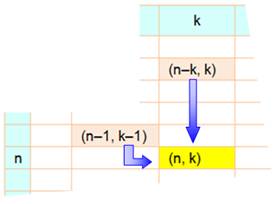
Relation de récurrence p(n, k) =
partition de n en k nombres entiers de 1 à k. |
Toujours valable, y compris pour
les partitions partielles
Valable pour le total des
partitions uniquement
avec p(n, k) = 0 si n < k et
p(n, n) = p(n, 1) = 1 |
||
|
Exemples Valeurs à lire dans les deux tableaux ci-dessus. p(10, 3) = p(9,
2) + p(7, 3) = 4
+ 4 = 8 p(17, 3) = p(16,
2) + p(14, 3) = 8
+ 16 = 24 |
Illustration
|
||
|
|
|||
|
Exemple avec n = 7 et m = 3. On cherche à
calculer p(7, 3), la quantité de toutes les partitions du nombre 7 avec les
nombres de 1 à 3. On liste ces permutations en ordre décroissant
des sommants (jaune). On les reporte à droite en distinguant deux groupes. En haut (bleu), il s'agit des permutations du
nombre 4 avec les nombres de 1 à 3. En bas (rouge), on reconnait la partition du
nombre 6 avec les nombres de 1 à 2. Le total des deux groupes donne la quantité des
partitions de 7 avec les nombres de 1 à 3. |
Les partitions sont reportées à droite en
isolant, en haut, le plus grand nombre k = 3 et en bas, le plus petit, le 1. Cette façon de faire isole des sous- partitions
plus petites dont la somme des quantités est la quantité cherchée |
||
|
|
Pourquoi deux formules? On trouve souvent la première formule en n – 1 dans la littérature. Elle marche bien pour
calculer le total des partitions. Elle est fausse pour le calcul des
partitions partielles avec les nombres de 1 à k seulement. Cet exemple montre comment la configuration 6 = 2 + 2 + 2 est ignorée par la formule en
n – 1.
Le programme qui suit utilie la formule en n. |
||
|
|
||
|
Programme mis en forme
Programme
pour copie dans Maple QP := proc (n, k) if n = k then return 1+QP(n, k-1) end if; if k = 0
or n < 0 then return 0 end if; if n = 0 or k = 1 then return 1 end if;
return QP(n, k-1)+QP(n-k, k) end proc; QP(7, 3); seq(QP(n, 3), n = 1 .. 10); seq(QP(7, k), k = 1 .. 7); |
Commentaires D'abord une procédure reprenant la formule de récurrence, puis le programme
principale qui appelle la procédure. La procédure est récursive: elle s'appelle elle-même. L'algorithme considère:
Le programme principal donne trois
exemples:
|
|
|
Trace du calcul de P(5, 3) par le programme
décrit ci-dessus
Rencontre
à cinq reprise du nombre 1: P(5, 3 ) = 5 |
|
|
Explications Partant de 5,3, la procédure passe les premiers
tests pour arriver à la formule de récurrence.
Il retient les deux résultats: P(5, 2) et (2, 3). Poursuite du travail avec
le premier et mise en mémoire du second. Appel à la procédure pour (5, 2) et création de
deux nouvelles valeurs: (5,1) et (3,2). Travail avec le premier et
mémorisation du second. Etc. Avec (5, 0), la deuxième condition est activée et
le programme passe son chemin sans action (0). Seul le cas m = k entraine une incrémentation de
la quantité de partitions. On en trouve 3 pour la partition de (5, 2) et 2
pour celle de (2, 3). Un total de 5. |
P(5, 3) = 5 |
Voir Récursivité
/ Quantité de partitions
(programme) / Programmation – Index
![]()
Table
obtenue avec le programme mentionné ci-dessus

Table établie avec un
tableur qui donne P(n, k =
m)
Même tableau que ci-dessus mais
avec la quantité de partitions pour chaque k
Ex: p(20, k = 4) ) = 64 (voir cases encadrées)

![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
Voir liste générale >>> |
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Addition/PttRecur.htm
|
![]()