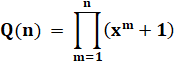NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 27/10/2020 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	ADDITION
Débutants Addition	PARTITIONS						Glossaire Addition
INDEX Partition Calculs	Approche			En bref et Index		S'y retrouver
	Formules de récurrence			Quantité de partitions		Partielles (1/2) – (2 / 2)
	Fonction génératrice			P(1) à P(6)	P(7) à P15)	K-Bonacci
	Digi-P	Diff-P		Bi-P	Tri-P	Pri-Bi-P		Pri-Tri-P
			Sommaire de cette page >>> Approche >>> Quantité >>> Fonction génératrice >>> Exercice de programmation

PARTITIONS

en sommes de nombres différents

PARTITIONS STRICTES

PARTITIONS IMPAIRES

Quelles sont les additions de nombres différents qui donnent la même somme ? Comme 1 + 4 = 2 + 3 = 5. On ne tient pas compte de l'ordre des termes de la somme.

La décomposition d'un nombre en sommes d'appelle sa partition. Ici, nous cherchons les partitions en nombres distincts.

La quantité de partitions strictes est égale à celle des partitions impaires.

Voir Partitions des nombres de 1 à 10 / Partitions avec k nombres différents

Approche

Observation: partitions distinctes (jaunes)

Le nombre 5 est sept fois somme de nombres inférieurs ou égal à 5.

Parmi ces sommes, seules trois sont formées de nombres distincts: Q(5) = 3.

Pour 6, il a onze partitions dont quatre avec des nombres distincts: Q(6) = 4.

Observation: partitions impaires (mauve)

Combien de partitions composées de nombres impairs uniquement ?

Quantité de partitions STRICTES

= quantités de partitions IMPAIRES

Partitions des nombres 5 et 6

5	1	1	1	1	1
		1	1	1	2
			1	2	2
			1	1	3
				2	3
				1	4
					5
6	1	1	1	1	1	1
		1	1	1	1	2
			1	1	2	2
				2	2	2
			1	1	1	3
				1	2	3
					3	3
				1	1	4
					2	4
					1	5
						6

Voir Table pour les nombres de 1 à 25

Quantité

Quantité pour n de 1 à 10

n	P	Q
1	1	1
2	2	1
3	3	2
4	5	2
5	7	3
6	11	4
7	15	5
8	22	6
9	30	8
10	42	10

Quantité successives des partitions distinctes

Exemple: pour n = 10, 10 partitions strictes et pour 19, il en a 54.

n	Q successifs
1 à 9	1, 1, 2, 2, 3, 4, 5, 6, 8,
10 à 19	10, 12, 15, 18, 22, 27, 32, 38, 46, 54,
20 à 29	64, 76, 89, 104, 122, 142, 165, 192, 222, 256,
30 à 39	296, 340, 390, 448, 512, 585, 668, 760, 864, 982,
40 à 49	1113, 1260, 1426, 1610, 1816, 2048, 2304, 2590, 2910, 3264,
50 à 59	3658, 4097, 4582, 5120, 5718, 6378, 7108, 7917, 8808, 9792,

Suite de cette table

Formule

La formule donne une approximation très grossière !

Réel: 1, 1, 2, 2, 3, 4, 5, 6, 8, 10, 12, 15, 18, 22, 27, 32, 38, 46, 54,

Calculée: 1, 1, 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 19, 23, 28, 33, 40, 47, 56

Réel: 3658, 4097, 4582, 5120, 5718, 6378

Calculée: 3753, 4201, 4699, 5250, 5860, 6535

Il existe des formules plus réaliste, mais faisant appel à des notions de maths très avancées (comme les fonctions hypergéométriques généralisées).

Fonction génératrice

Le polynôme générateur est le produit des monômes (x^m + 1).
La quantité de partitions strictes de n est le coefficient du degré n du polynôme développé.

m	C(x^n)	PG(n)
1	1	(1 + x) (x^2+ 1) = x^3 + x^2 + x + 1
2	1	(1 + x) (x^2+ 1) (x^3+ 1) = x^6 + x^5 + x^4 + 2 x^3 + x^2 + x + 1
3	2	(1 + x) (x^2+ 1) (x^3+ 1) (x^4+ 1) = … + 2 x^4 + 2 x^3 + x^2 + x + 1
4	2	… + 3 x^5 + 2 x^4 + 2 x^3 + x^2 + x + 1
5	3	… + 4 x^6+ 3 x^5 + 2 x^4 + 2 x^3 + x^2 + x + 1
6	4	… + 5 x^7 + 4 x^6 + 3 x^5 + 2 x^4 + 2 x^3 + x^2 + x + 1

Programme Maple

Commentaire

La procédure extrait le coefficient de rang n du polynôme générateur.

Réalisation du produit des monômes et demande de la forme développée avec expand.

L'instruction coeff extrait le coefficient de rang n dans le polynôme.

Le programme principal établit la suite (seq) des coefficients extraits par PS pour i de 1 à 15.

Résultat imprimé en bleu.

Voir Programmation – Index

Exercice de programmation
Programme Maple	Exercice La quantité de partitions strictes peut se calculer en utilisant la fonction génératrice. Cet exercice propose de balayer toutes les partitions et de ne retenir que celles avec des nombres différents. Procédure d'identification d'une partition stricte Appel de isdif (est différent) pour une liste L. Elle est transformée en un ensemble S (les éléments répétés sont éliminés). Comparaison de la quantité d'éléments dans L et S. Si identique, c'est qu'il n'y avait pas de doublons et, donc que tous les chiffres étaient différents. On retourne vrai (true). Programme principal La variable mx indique l'extension de la recherche. Exploration des nombres de 1 à mx. Pour chacun partition (sous combinat) donne toutes les partitions du nombre n. Boucle d'exploration de chacune (p) de ses partitions. Si elle est stricte, elle est enregistrée dans la liste PD. Impression en fin de programme de n, de la quantité de partitions, de la quantité de partitions strictes et de ces partitions strictes.

SUITE: Démonstrations >>>

Retour	Digi-Partition Partition sous contraintes Partitions avec k nombres différents
Suite	Table des partitions strictes pour les nombres de 1 à 25 Bipartition / Partitions – Index
Jeux	Fubuki / Kakuro
Voir	Addition - Glossaire Addition des carrés Addition des entiers Addition des puissances Carrés magiques Conjecture de Goldbach	La magie du carré 3 x3 Multi-somme de puissances Partition de 15 S'y retrouver Totient d'Euler
Sites	Partition d'un entier – Wikipédia Partition function Q – Wolfram MathWorld OEIS A000009 - Expansion of Product_{m >= 1} (1 + x^m); number of partitions of n into distinct parts; number of partitions of n into odd parts
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Addition/PttDiff.htm