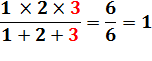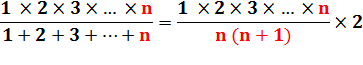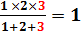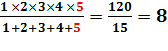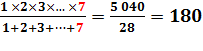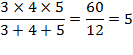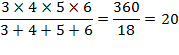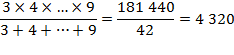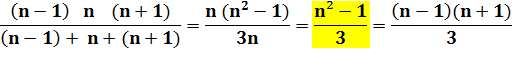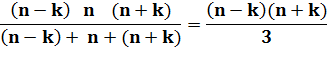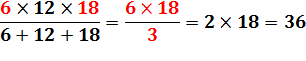|
|||||||||||||||||||||||||||||
![]()
|
DIVISIBILITÉ & CURIOSITÉS Divisibilité d'un produit
par la somme de ses termes. Comme:
Ce type de fraction – factorielle 3 divisée par la somme de ses termes – égale à 1 est unique. Question: peut-on en trouver d'autres avec un
nombre entier comme quotient? |
Voir Nombre
entier / quotient /
consécutifs
|
des nombres consécutifs de 1 à n |
|
|
|
SOMME |
PRODUIT |
|
|
S = (n+1) n / 2 |
5! = 1 x 2 x 3 x 4 x 5 = 120
n!
= n (n-1) (n-2) … 2 x 1 |
|
|
1,
3, 5, 7, 8, 9, 11, 13, 14, 15, 17, 19, 20, 21, 23, 24, 25, 26, 27, 29, 31,
32, 33, 34, 35, 37, 38, 39, 41, 43, 44, 45, 47, 48, 49, 50, 51, 53, 54, 55, 56,
57, 59, 61, 62, 63, 64, 65, 67, 68, 69, 71, 73, 74, 75, 76, 77, 79, 80, 81,
83, 84, 85, 86, 87, 89, 90, 91, 92, 93, 94, 95, 97, 98, 99, … Soit 76 valeurs sur 100. |
||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Observation
La somme ne divise pas la factorielle si n+1 est un
nombre premier impair. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
La
somme des nombres de 1 à n divise factorielle n - sauf lorsque n+1 est un nombre premier
impair - et,
le rapport est pair. |
|
|
||
|
|
||
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
6 |
|
|
|
7 |
|
|
|
8 |
|
|
|
9 |
|
|
|
10 |
|
|
|
11 |
|
|
|
12 |
|
|
|
On
notera la superbe relation:
Basée
sur la propriété unique:
|
Voir Pépites
|
|
|
|
4 + 5 + 6 = 3 x
5 = 15
(n – 1) n (n + 1) = n (n² – 1) = n3 – n Il suffit donc de prendre le cube du facteur central et
d'y retrancher ce terme: 4 x 5 x 6 = 53
– 5 = 125 – 5 = 120
Faire
le produit des extrêmes et diviser par 3. |
|
Voir Calcul
mental / Divisibilité de trois nombres
consécutifs / Consécutifs
![]()
|
Suite |
|
|
Voir |
|
|
Accès aux nombres |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Decompos/DivisiXY.htm
|
![]()
Renvoi de liens (textes déplacés)
DIVISIBILITÉ par 222 >>>
DIVISIBILITÉ DE DIFFÉRENCE DE PUISSANCES >>>