|
Édition du: 23/10/2022 |
|
INDEX |
SOMME & PRODUIT |
||
|
Somme
et produit des chiffres – Index |
|||
Faites un double-clic pour un retour en haut de page
![]()
|
Trouver k nombres connaissant la SOMME et le PRODUIT La somme
de ces nombres est 12 et leur produit 36. Trouver ces nombres. Comment
s'y prendre pour trouver ces nombres. Y-a-t-il toujours une ou plusieurs
solutions ? |
||
|
|
Sommaire de cette page >>> Approche – Exemple 1 >>> Approche – Exemple 2 >>> Solution >>> Toutes des possibilités S1-21 et P20-40 >>> P = 300 –Toutes les sommes possibles >>> Bilan >>> Exemple de recherche |
Débutants Glossaire |
Rappel pour deux nombres
|
1)
Équation à résoudre 2)
Identités remarquables Exemple: 3)
Formule rapide Si x + y = 2m et xy = p, alors:
Exemple avec S pair: S = 16 P = 55
Exemple avec S impair: S = 17 P = 42
4)
Méthode valable aussi pour k nombres Seuls ces nombres peuvent intervenir dans la somme. On devine rapidement qu'il s'agit de 5 et 11. |
|
On connait la somme de k nombres et leur produit. Déterminer ces nombres. |
Exemple Somme S =
11 Produit P = 30 Deux solutions:
5 + 6 et 1 + 2 + 3 + 5 |
|
|
Les diviseurs du nombre-produit sont les seuls
termes possibles de l'addition. Les sommes ne peuvent être construites qu'avec
certains de ces nombres. On note que choisir le 1 dans la somme ne change
pas le produit. |
Facteurs 30 = 1 × 2 × 3 × 5 Diviseurs 1, 2, 3,
5, 6, 10, 15, 30 |
|
|
Quelles sont les partitions possibles utilisant
certains des diviseurs. Cinq sommes sont possibles, mais deux seulement
arrivent au produit demandé (en rose). |
Solutions S = 11 = 10 + 1 P = 10 |
|
|
Trouver les nombres tels que S = 20 et P = 300. |
Diviseurs de 300 1, 2, 3,
4, 5, 6, 10, 12, 15, 20, 25, 30, 50, 60, 75, 100, 150, 300 |
|
|
Partitions de 20 Il existe 627 partitions du nombre 20. Après investigations, il n'en reste que quatre
recevables. On peut restreindre la recherche à des nombres distincts, auquel cas, il n'y en a qu'une seule
solution: 20 = 10 + 5 + 3 + 2 dont le produit est 300. |
Partition avec les diviseurs 20 = 15 + 5 |
|
|
Pas toujours de solutions Disons- le tout de suite: il n'y a pas toujours
de solutions. C'est même rarement le cas. Avec le produit P = 30, seuls sept nombres de 1 à
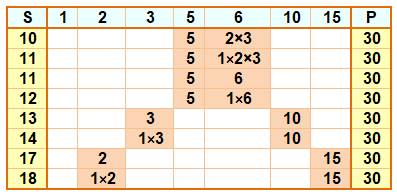
30 ont des solutions avec nombres distincts, dont deux pour le nombre 11 (voir tableau). Notez que P doit être un nombre composé. Sinon,
la somme est automatiquement ce nombre. Choix des diviseurs à ajouter On observe que le choix des diviseurs
pour réaliser la somme se fait par couples avec symétrie, comme le montre ce
tableau pour P = 30:
Cette observation est très utile pour limiter le
champ des recherches. |
Seules solutions pour S de 1 à 30 Produit P = 30 S = 10: 2, 3,
5 11: 5, 6 11: 1, 2, 3, 5 12: 1, 5, 6 13: 3, 10 14: 1, 3, 10 17: 2, 15 18: 1, 2, 15 |
|
|
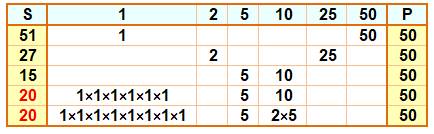
Exemple de recherche On cherche la solution de S = 20 et P = 50 Duplication autorisée. Ici les deux solutions
possibles comportent respectivement cinq et huit fois le nombre 1.
On comprend que cette possibilité de duplication
soit bannie ! |
Solutions avec de nombreux 1 Produit P = 50 Somme S = 20: Deux solutions 1, …15 , 5, 10 1, …18 , 2, 5 , 5 |
|
Tableau de toutes des possibilités pour S de 1
à 25 et P de 20 à 40

|
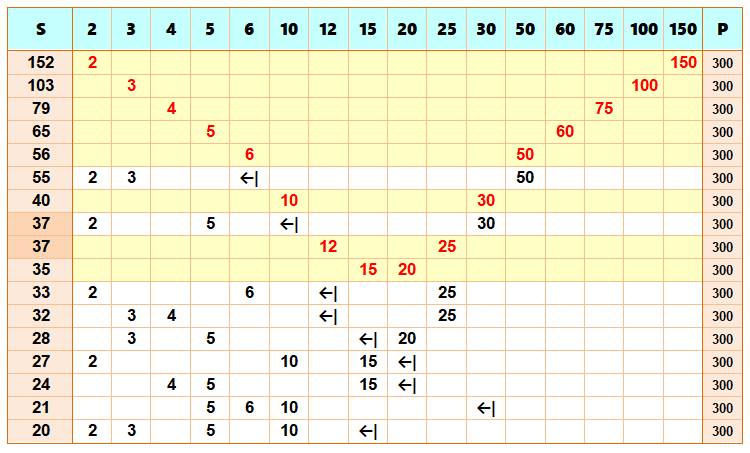
Sur la ligne du haut (bleue), les seize diviseurs
propres de 300 (sans 1 et 300). Chaque ligne correspond à un choix de diviseurs
dont le produit est 300. Ces lignes ont été triées par sommes
décroissantes. Les lignes jaunes correspondent à un produit de deux facteurs; les blanches
à la factorisation du diviseur indiqué par la flèche: Ainsi 6 × 50 devient 2 × 3 × 50.
Notez Seule la somme 37
apparait deux fois: 12 + 25 = 2 + 5 + 30. Les sommes (S + 1) sont aussi des solutions. En
effet, en ajoutant 1, le produit reste le même. |
|
|
La solution pour
S et P donnés au hasard est rare. Lorsqu'elle
existe, elle est souvent unique. Pour trouver la solution,
on réalise la somme deux à deux des diviseurs donnant le produit et on
poursuit en factorisant les diviseurs composés. On évite de compter les
doublons. L'aide d'un tableur est
appréciable. |
|
Trouver les nombres tels que: |
Diviseurs de 311 190 Ce nombre est divisible
par 10 = 2 × 5. Il est divisible par 3: (3+1+1+1+9) et 31119/3 =
10373 Ce nombre est divisible par 11: (1+3+3 = 0+7) et
10373 = 943 Les critères de divisibilité ne donnent plus
rien. Soit la factorisation: 311 190 = 2 × 3 × 5 × 11 × 23 × 41 Somme La somme vaut: 2 + 3 + 5 + 11 + 23 + 41 = 85. Quelques essais permettent de trouver: 2 + 3 + 5
+ 11 x 23 + 41 = 304 Solution Les nombres sont alors: 2, 3, 5, 253, 41. |
|
Merci
à Jérôme Rampon pour l'idée de cette page
Haut de page (ou
double-clic)
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |