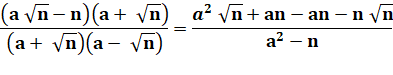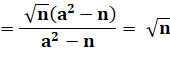collection de nombres, calcul des fractions continues

NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 13/01/2024 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	FRACTIONS
Débutants Fractions	Fractions continues			Glossaire Fractions
INDEX Fractions Calculs	Généralités	Valeurs	Pell (résolution)	Analogie rectangle
		Calcul	Ramanujan	Calendriers
		Propriétés	Rogers-Ramanujan	Engrenages
		Sommaire de cette page >>> Exemple de calcul avec pi >>> Méthode par divisions successives >>> Calculs avec Maple >>> Cas des racines

FRACTIONS CONTINUES

CALCULS

Exemple de calculs et utilisation d'un logiciel de calcul.

2,3130367364
3358290638 3951602641
7824763 …

La fraction continue de ce nombre produit tous les nombres premiers.

Voir Nombre 2,3130…

Calcul pour Pi

= 3, 141 592 653 589 793 2385 …

Calcul




	3	7

La fraction 355/113 est une approximation courante de Pi. Les fractions obtenues à partir du calcul des fractions continues sont appelées des réduites de Pi (Anglais: convergents).

Fraction continue de Pi

Voir suite des composantes en Valeurs

Réduites de Pi

Formule de Brouncker

Méthode de calcul par divisions successives

Comment trouver cette fraction continue ?

111 / 11 = 10, 090909...

= [10 ; 11]

Calcul

1) On divise normalement 111 / 11

111	11
1	10

Résultat 10 reste 1

2) Le diviseur 11 devient le dividende de l'opération suivante : 11 / 1

11	1
0	11

Résultat 11 reste 0

3) Poursuivre jusqu'à obtenir un reste nul.

Ce qui est déjà le cas dans cet exemple simple.

Notation en division cascade

	111	11
11	1	10
0	11

Autre exemple, avec la notation

200 / 111 = 1,801 801...

= [1 ; 1, 4, 22]

			200	111
		111	89	1
	89	22	1
22	1	4
0	22

Fractions continues d'une racine
Méthode avec numérateur unité Exemple avec racine de 5.
Calcul de (1 / (rac5 – 2): inverse de la partie décimale.
Toujours: inverse de la partie décimale.
Mêmes décimales.
La poursuite du calcul montre que la nombre 4 est répété à l'infini:

Méthode avec numérateur imposé	Exemple avec l'année de naissances: 1970.
Elle repose sur l'identité suivante:
Explication: réduction au même dénominateur
Multiplication par le conjugué pour éliminer le radical du dénominateur
Avec n = 1970 et a = 1 Pour info: la fraction continue classique avec 1 au numérateur: [44, 2, 1, 1, 2, 88, 2, 1, 1, 2, 88, 2, 1, 1, 2, 88, …]
Méthode de calcul Calcul de la première fraction avec une "semence", une racine approchée de n (ici on prend s = 44, par exemple). Cette valeur calculée devient s, et elle est réinjectée dans la formule et cela autant de fois que vous voulez.		Intérêt pour l'amusement: les fractions successives oscillent beaucoup avant de converger vers la racine. Après 300 itérations, on arrive à 44,3846825 pour 44,3846820.

Calculs avec Maple
Conversion d'un rationnel ne faction continue: instruction confrac. Conversion de Pi avec 20 termes Conversion du nombre d'or (Phi) avec 11 termes (par défaut).
Obtention des réduites
Conversion d'une fraction continue en rationnel La fraction continue dont les termes sont tous égaux à 2 est égale à 1 + racine de 2. Maple sait reconnaitre certains nombres avec l'instruction: identify. Avec des 4, la fraction continue représente le nombre 2 + racine de 5.