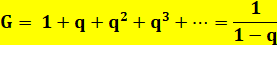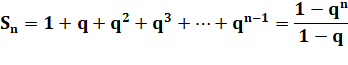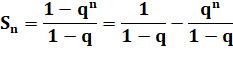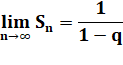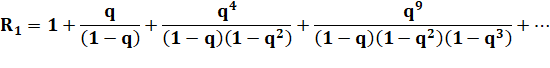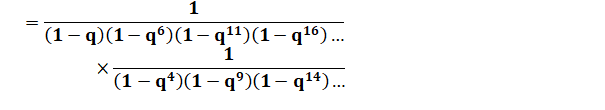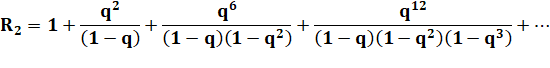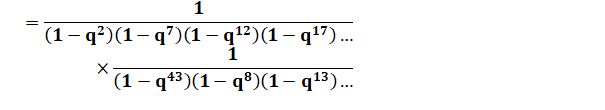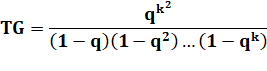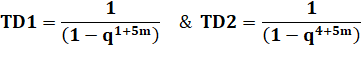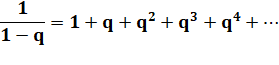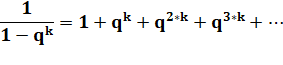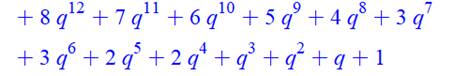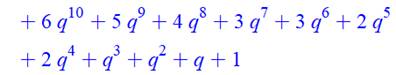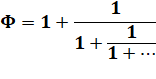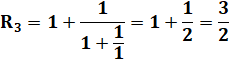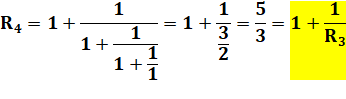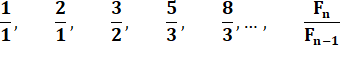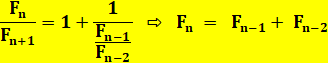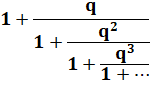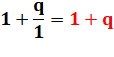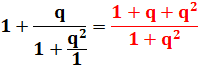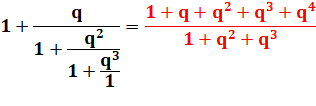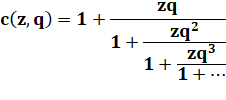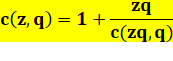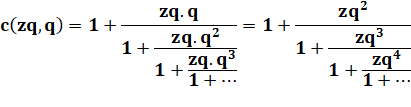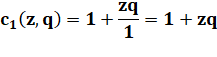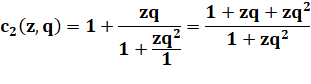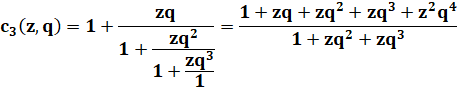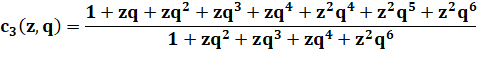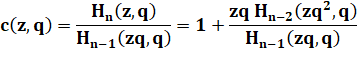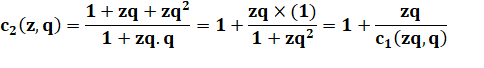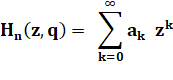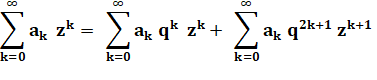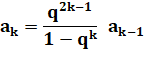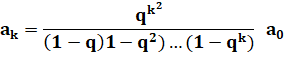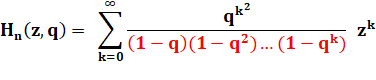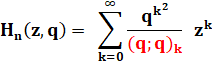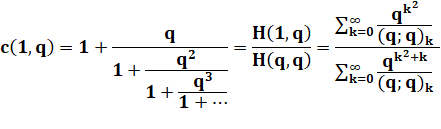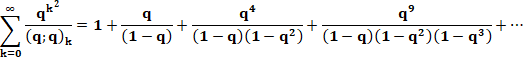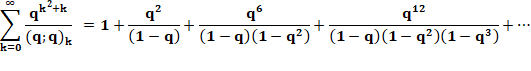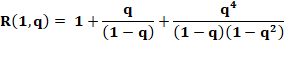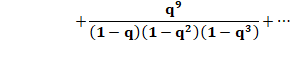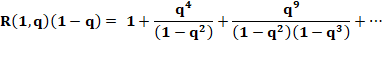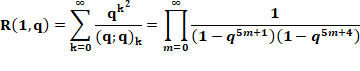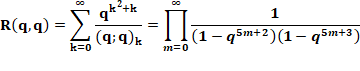|
||||||||||||||||||||||||||||||||||||||||
![]()
|
IDENTITÉS & FRACTIONS CONTINUES de ROGERS-RAMANUJAN Deux identités expliquées qui
conduisent aux fractions
continues spéciales de Rogers et de Ramanujan. Cette fraction continue n'est
généralement pas d'un abord facile. La démarche de Gaurav
Bhatnagar, mathématicien indien, m'a semblé simple et logique, même si la
fin du raisonnement est d'un niveau élevé. Laissez-vous guider pour découvrir
cette magnifique œuvre. |
|
En 1913,
Ramanujan, alors un employé indien inconnu,
envoie ses lettres à Hardy, un
mathématicien britannique, qui les trouva époustouflantes: "elles me
renversèrent complètement; Pour le moins, je n'avais jamais vu quelque chose
de cette sorte avant (they defeat me completely; I had never seen anything in
the least like them before)". Parmi les
beautés trouvées, les identités, objet de cette page, circulèrent parmi les
mathématiciens, mais personne, Ramanujan compris, n'était capable de les
démontrer. Un jour,
lisant de vielle coupure de journaux, Ramanujan tombe sur un article édité en
1894 par un mathématicien anglais nommé Leonard Rogers (1862-1933). En
s'associant, les deux mathématiciens éditèrent la démonstration de ces
identités en 1919. En 1917,
Schur les recouvre. |
|
Série
géométrique pour |
Exemple: avec q = ½, G = 2 Le calcul
jusqu'à q6 donne 1,9843…. |
|
|
Prenons
la série finie: |
|
|
|
Démonstration
en multipliant par (1 – q). |
|
|
|
On peut
aussi l'écrire: |
|
|
|
Limite
pour n infini, Avec qn
tendant vers 0: |
|
|
|
|
||
|
Forme générique Les
termes à gauche de l'égalité sont du type: |
|
|
|
Ceux de
droite sont de deux types: |
|
|
|
Vérification de l'égalité Il est
possible de calculer ces termes en remplaçant
chaque fraction par la somme infinie équivalente. |
|
|
|
En se
limitant à q10 et aux expressions
telles qu'indiquées on trouve pour les premiers termes suivants. (Calculs exécutés avec le
logiciel Maple) |
À gauche
À droite
|
|
Faisons le point
|
Nous
venons d'aborder deux identités qui semblent bien élégantes, certes; mais à
quoi peuvent-elles bien servir. Nous allons les retrouver à la fin de notre
exploration des fractions continues spéciales introduites par Rogers et par
Ramanujan. |
|
|
||||
|
Fraction continue classiques Fraction
continue du nombre d'or: |
|
|||
|
Calcul
des réduites (exemple). Voyez
comme il est facile de passer d'une réduite à la suivante. |
|
|||
|
Réduites
successives: on y retrouve les nombres
de Fibonacci. Elles
conduisent à la formule de récurrence et à définition des nombres de
Fibonacci. |
|
|||
|
Fraction continue généralisée Introduction
d'un facteur q au numérateur avec une puissance correspondant à son étage. |
|
|||
|
Calcul
des réduites: Note: pas facile de passer directement d'une réduite à la suivante comme
pour les fractions continues classiques. Peut-on trouver un truc pour
y arriver tout de même? |
|
|||
|
Fraction continue de Rogers-Ramanujan Introduction
d'un paramètre z. |
|
|||
|
La récurrence est alors
possible, comme nous allons le voir. |
|
|||
|
Calcul des réduites: Une relation semble se
dégager entre le numérateur de l'un et le dénominateur du suivant. |
|
|||
|
Appelons Hn(z,q)
le numérateur |
Exemple:
|
|||
|
Soit la relation de
récurrence générique, en multipliant par Hn-1. |
|
|||
|
Pour résoudre cette
identité, on suppose que H est égal à une série (somme infinie). |
|
|||
|
Nouvelle relation de
récurrence avec ces séries. |
|
|||
|
Comparaison des
coefficients: |
|
|||
|
En itérant de k – 1 jusqu'à 0, on trouverait: |
|
|||
|
En prenant a0 = 1 Voyez la notation adoptée. |
|
|||
|
Retour à la fraction
continue généralisée (avec z = 1) |
|
|||
|
Conclusion |
La
fraction continue de Rogers-Ramanujan est le rapport entre ces deux sommes. Sommes que nous avons déjà vues en début de page. Nous
savons que toutes deux se transforment également en produits. |
|||
|
|
||
|
La gauche
de notre première identité |
|
|
|
Avec la conversion en séries
géométriques: |
|
|
|
En
multipliant par (1 – q) |
|
|
|
On
continue |
|
|
|
Finalement |
|
|
|
Les
puissances sont en 5m+1 ou 5m+4. On devine
les deux identités suivantes; ce sont celles énoncées en début de page, mais
avec les notations introduites ci-dessus. |
||
|
Identités de Rogers-Ramanujan |
|
|
![]()
|
Suite |
|
|
Voir |
|
|
|
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Identite/Ramanuja.htm
|
![]()