Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 13/01/2023 M'écrire Brèves de Maths

INDEX Nombres premiers Types de nombres	Nombres premier – Quantité
	Quantité	Fonction Pi (n)	Théorème des NP
	Historique de Pi (n)	Tables Pi (n)	Intervalle minimum
	Quantité de jumeaux	Premiers de Ramanujan	Encadrement

Faites un double-clic pour un retour en haut de page

NOMBRES PREMIERS Encadrement – Bornes On connait approximativement le nombre premier p de rang n. Ici, on se pose la question de savoir quel est l'intervalle dans lequel on est sûr de le trouver. Quelles sont les formules qui précisent la borne inférieure comme la borne supérieure ? Notion d'encadrement de la valeur du nombre premier. Nous allons prendre une démarche expérimentale; pour une explication sur la démarche théorique s'en remettre aux sites cités en référence (niveau avancé, fonction de Tchebychev).
	Sommaire de cette page >>> Approche – Approximation de p >>> Encadrement classique >>> Encadrement avec constante >>> Encadrement avec fonction >>> Bilan – Formules (théorèmes) >>> Encadrement le plus performant (2017) >>> Historique	Débutants Nombres premiers Glossaire Nombres premiers

NP: Nombres premiers

Anglais: Rosser's theorem; lower bound; upper bound

Approche – Approximation du énième premier		haut
Le théorème des nombres premiers nous renseigne:	Le nombre premier p de rang n est approximativement égal au rang multiplié pat son logarithme naturel.
Amélioration avec termes complémentaires en logarithmes doubles.	Le nombre premier est à peine supérieur à cette expression avec un logarithme de logarithme, parfois noté ln2(n)
Et même mieux: Cipolla en 1902. Formule valable pour de très grands nombres premiers (valeur asymptotique).	Voir Formule performante
Exemples Ces trois formules produisent des nombres inférieurs aux nombres premiers. En rouge, chiffres significatifs rendus par la formule.

Voir Quantité de nombres premiers / Brève 47/929

Encadrement classique		haut
Postulat de Bertrand – Théorème de Tchebychev Entre n et 2n, il existe toujours un nombre premier.	Borne maximale pour le énième nombre premier p(n) < 4^n
Conséquence Il existe n nombres premiers entre 1 et 2^n. La table montre le énième nombre premier p(n) et la quantité Q de nombres premiers entre 1 et 2^n. La colonne p(d) indique le dernier nombre premier inférieur à la limite 2^n. On note que p(n) << Q Le nième premier est très inférieur à 2^n.

Encadrement avec constante		haut
Sur ce graphique, les nombres premiers p sont représentés par la courbe bleue. Les courbes verte et rouge encadrent la bleue, au moins à partir du cinquième nombre premier (p = 13).	Comparaison des nombres premiers avec deux courbes enveloppes Courbe verte: K = 0; courbe rouge: K = 1
On peut chercher à resserrer l'encadrement avec des valeurs de K comprise entre 0 et 1. On représente ici, les écarts par rapport aux nombres premiers (barre noire sur l'axe des x). En bleu, on retrouve les deux situations précédentes avec K = 0 et K = 1. Si la courbe K = 0,9 reste en dessous de la barre, les deux autres la croisent et ne peuvent pas prétendre à un encadrement du moins pour ces valeurs des nombres premiers.	Écart pour K de 0 à 1 pour les nombres premiers de 3 à 229

Encadrement avec fonction		haut
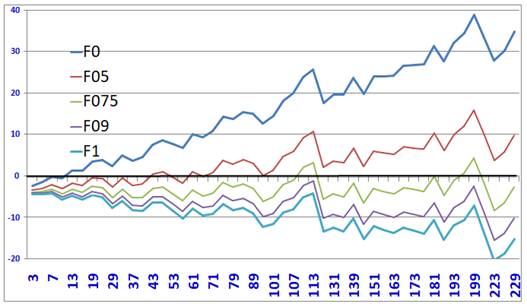
Idée Avec la constante K fixe les courbes, aussi proches soient-elle, s'éloignent avec des nombres premiers de plus en plus grands. L'idée consiste à rendre cette valeur variable en fonction du rang n.	Résultat Sur les courbes ci-dessous, hors, la courbe verte (F = 0,75), les quatre autres enveloppent la barre des premiers, à partir d'une certaine valeur.
Écart pour F de 0 à 1 pour les nombres premiers de 29 à 15 millions (par échantillonnage avec un pas de 10 000) Avec F valant: 0; 0,5; 0,75; 0,9; 1.

Bilan – Formules

haut

Borne inférieure

Constante

Avec -1 et ln

n	p(n) MINIMUM
> 1*
> 1*	Prouvée si l'hypothès de Riemann est admise.
> 1*
n > 8 600*

> 1*
2 ≤ n < 21 466**
21 466 ≤ n < 688 383**
688 383 ≤ n*

* Théorèmes (démontrés); ** Proposées par Jean-Philippe Pène

Borne supérieure

Constante

Avec -1 et ln

n	p(n) MAXIMUM
> 5
> 19
> 109
> 2 193
> 8 601
> 15 985*

> 5*
> 12*
2 ≤ n < 70**
70 ≤ n < 712 **
712 ≤ n < 688 383**
27 076 ≤ n*	Prouvée si l'hypothès de Riemann est admise.
688 383 ≤ n*

* Théorèmes (démontrés) ; ** Proposées par Jean-Philippe Pène

Encadrement le plus performant (2017)

haut

Point des recherches En 1902, M. Cipolla propose cette formule générale: M. Cipolla, La determinazione assintotica dell’ n^imo numero primo Le terme en Sigma se décline pour les valeurs successives de k. En 2017, Christian Axler – Démontre les formules ci-dessous pour k = 2. Voir Historique Formules n ≥ 46 254 381 n ≥ 2 Voir Brève 47/929 Exemples pour n en puissances de 10 En jaune, valeurs de n pour lesquelles les formules s'appliquent.

Voir Nombres premiers de rang 10^k

Historique

1896 – Hadamard et De la Vallée Poussin, indépendamment, démontrent le théorème des nombres premiers: p(n) ≈ n ln(n) – Valeur asymptotique pour n tendant vers l'infini.

1902 – M. Cipolla améliore ce résultat avec une formule en p(n) = n (ln(n) + ln₂(n) – 1 + Σ …). Ce qui implique que p(n) > n ln(n); p(n= < n (ln(n) + ln₂(n)); p(n= > n (ln(n) + ln₂(n) – 1); etc. avec plus de termes et cela à partir d'un certain n.

1939 – John Rosser: théorème de Rosser: le énième nombre premier p(n) vérifie: p(n) ≥ n ln(n). Il montre également que p(n) < n(ln(n) + 2 ln₂(n) pour n > 3.

1962 – Rosser et Schoenfeld: p(n) ≤ n ((ln(n) + ln₂(n) pour n > 5.

1975 – Rosser et Schoenfeld: p(n) ≥ n (ln(n) + ln₂(n) – K) avec K = 3/2. puis cette constance est réduite à C = 1,0072629 par Robin.
Ils montrent également que p(n) < n (ln(n) + ln₂(n) – 0,5) pour n > 19.

1983 – Robin donne: C = 1 pour 1 < n ≤ e⁵⁹⁸ et pour n ≥ e¹⁸⁰⁰.

1996 – Jean-Pierre Massias et Guy Robin proposent des bornes effectives pour les nombres premiers. C'est la majorité des formules démontrées citées ci-dessus. Cf. page 218

1999 – Pierre Dusart démontre que C= 1 est valable pour tout n > 1.

2017 – Christian Axler – Démontre les formules en ln₂² vues ci-dessus (meilleure performance).

Haut de page (ou double-clic)

Suite	Historique de Pi(n) Fonction Pi (n) Énième nombre premier Propriétés des nombres premiers Hypothèse de Riemann Nombres premiers – Index FAQ sur les nombres premiers
Voir	Liste de nombres premiers Consécutifs Facteurs premiers autour de 1000 Jumeaux Nombres composés Premiers en tableaux, en spirales … Représentation des nombres Séquences
Sites	Fonction de compte des nombres premiers – Wikipédia Prime counting function – Wolfram MathWorld The Nth Prime page – Andrew Booker – Pour connaitre le énième nombre premier OEIS A000720 – pi(n), the number of primes <= n Rosser's Theorem – Wolfrma MathWorld Théorie (** signifie: niveau universitaire) Explicit bounds for some functions of prime numbers – Barkley Rosser -1941 Bornes effectives pour certaines fonctions concernant les nombres premiers** – Jean-Pierre Massias et Guy Robin - 1996 Autour de la fonction qui compte le nombre de nombres premiers** – Pierre Dusart – 1998 The kth prime is greater than …** – Pierre Dusart – 1999 (réf 1) New estimates for nth prime number** – Christian Axler – 2017 New estimates for nth prime number** – Christian Axler – 2019
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Premier\Encadrem.htm