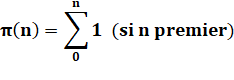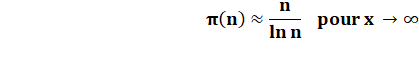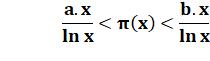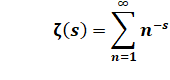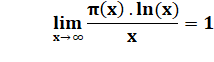|
|||||||||||||||||||||||||||||||||||||||||||||
NP: Nombres premiers
![]()
|
Quantité de nombres premiers HISTORIQUE |
Voir Historique sur les nombres premiers
|
|
|
|
On note
qui veut dire: somme de 1 autant de fois
que de nombres premiers p inférieurs ou égaux à n
|
|
|
|
|
|
Théorème des nombres premiers
Cad: Le nième nombre premier, pour n très grand, est
dans le voisinage de n x ln n. Exemple: le millième nombre premier est 7 919
et 1000. ln 1000 = 6 908 erreur de 12% Avec le millionième nombre
premier on atteint 10,78 % d'erreur. Gauss (1777-1855)
et Legendre (1752-1833) En 1798,
Legendre publie la première
conjecture sur Dans son livre Essai sur la
Théorie des Nombres, il indique : " La valeur de 1,08366 tient à la
dimension des tables de premiers disponibles à l'époque. En fait, on obtient
une meilleure approximation avec simplement 1. Exemple: Avec le millième nombre premier, on obtient 7907 au lieu de 7 991 (0,9
%) Avec le millionième nombre
premier on est encore avec 3 % d'erreur. En 1863,
une lettre de Gauss (1791 et 1849) est
publiée et donne : (x) est
approximativement Li(x), l'intégrale de 1/log t de t = 2
à t = x. |
|
Voir Décompte des nombre
premiers de Legendre
|
|
|
|
Avec a
= 0,921 et b = 1,106 pour x grand Et que, s'il y a
une limite pour a et b, ce sera 1.
|
|
Voir Chronologie des pe rsonnalités
|
|
|
|
Tomas Oliveira e Silva calcule
|
|
![]()
Fonction de compte de Legendre – Texte écrit
par Joseph Pasquier
|
|
![]()
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
|
|
|
Cette page |
![]()
Livres célèbres (théorie
des nombres: attention niveau élevé)
|
LES
NOMBRES PREMIERS (théorie
analytique moderne des nombres premiers) |
Gérard Michel |
Tenenbaum Mendès
France |
Que
sais-je? N°
571 |
1997 |
|
Les
nombres premiers (avec méthodes algébriques) |
Jean |
Itard |
Que
sais-je? Deuxième
édition |
1969 |
|
Les
nombres premiers |
Émile |
Borel |
Que
sais-je? Première
édition |
1953 |
Voir Biblio