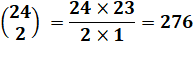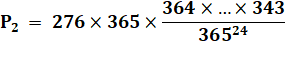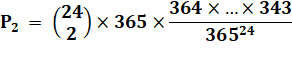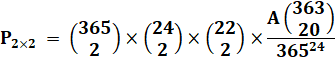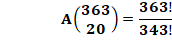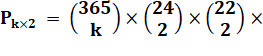NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 22/04/2021 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	PROBABILITÉS
Débutants Dénombrement	Général			Glossaire Probabilités
INDEX Probabilités et statistiques Nombre en grand nombre	Probabilités	Grands nombres	Pile ou Face	Famille
		Moyenne & Médiane	Dés	Anniversaire 2
		Coïncidences	Historique	Anniversaire 3
		Sommaire de cette page >>> Approche >>> Trois anniversaires, 24 personnes – Avec hypothèse >>> Trois anniversaires, 24 personnes – Sans hypothèse

ANNIVERSAIRES à 3

Trois personnes, au moins, parmi n

ont leur anniversaire le même jour

On sait calculer la probabilité d’avoir deux personnes parmi n ayant leur anniversaire le même jour. Quel est le calcul pour trois ?

On peut encore faire un calcul combinatoire pour trois. Pour quatre ou plus, il faudra faire confiance à la loi de Poisson qui donne une très bonne approximation.

Anglais : The three birthday problem / Situation where three people have the same birthday

Résumé

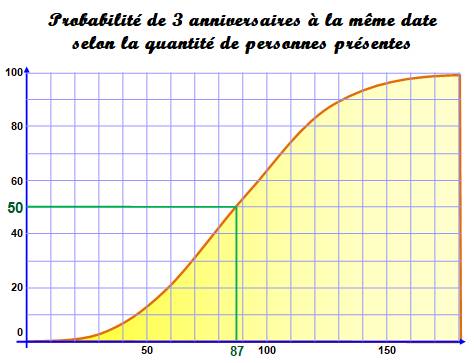
Pour obtenir une probabilité de 50%, il faut:

23 personnes dans la salle pour 2 anniversaires le même jour, et

87 ou 88 personnes pour 3 anniversaires le même jour (49,94... pour 87 et 51,10… pour 88).

Avec 23 personnes la probabilité de trouver 3 anniversaires le même jour est faible : 1,5 %.

Multi-anniversaire

Nombre minimum n de personnes pour avoir 50 % de probabilité d'avoir k anniversaires le même jour. L'indice indique la valeur de k.

Ainsi, il faut au moins 623 personnes dans une assemblée pour avoir une chance de 50% de trouver sept personnes avec le même jour anniversaire (la même date, pas la même année)

1, 23₂, 88₃, 187₄, 313₅, 460₆, 623₇, 798₈, 985₉, 1181₁₀, 1385, 1596, 1813, 2035, 2263, 2494, 2730, 2970, 3213, 3459, 3707, 3959, 4213, 4470, 4728, 4989, 5252, 5516, 5783, 6051, 6320, 6592, 6864, 7138, 7413, 7690, 7968, 8247, 8527, 8808, 9090, 9373, 9657, 9942, 10228, …

OEIS A14088

Approche
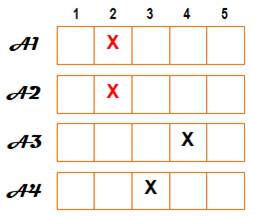
Supposons un groupe de quatre personnes (A1 à A4) toutes nées parmi les cinq jours de lundi à vendredi. Le graphique indique les anniversaires des quatre personnes selon le numéro du jour. La situation présentée montre que trois personnes ont leur anniversaire le deuxième jour. La personne P4 peut avoir son anniversaire un des cinq jours, le cas où les quatre ont le même jour anniversaire est permis.
On sait calculer la probabilité qu’exactement deux personnes parmi cinq aient leur anniversaire le même jour. L’idée est de calculer la probabilité d’avoir des anniversaires différents pour les deux autres. Ceux qui restent sont ceux qui partagent le même anniversaire à trois ou quatre.
Probabilité de deux avec anniversaires différents : Pour le 1^er: 1 parmi 5 Pour le 2^e : 1 parmi 4 Pour le 3^e : 1 parmi 3 Pour le 4^e : 1 parmi 2
Probabilité de deux anniversaires exactement à la même date : On a 2 choix parmi 4 pour ces deux individus, soit 6 possibilités. Ces deux ont un anniversaire parmi les cinq dates (resteront quatre dates), les deux autres doivent avoir des anniversaires différents. La quantité de tous les cas possible est toujours 5^4.
Probabilité pour que trois personnes parmi quatre aient le même jour anniversaire parmi cinq dates :
Tests par ordinateur sur cinq fois un million de tirages :	0,232676 0,231617 0,231275 Moyenne : 0,232 0,231201 0,232931

Principe de la suite du calcul

Dans le cas de quatre personnes, nous avions un couple avec même anniversaire. Dans le cas de plus de personnes, il peut y avoir plusieurs couples en même temps.

On va d’abord faire le calcul avec l’hypothèse (fausse) qu’il n’y a pas d’autres couples. Le calcul est le même que celui vu ci-dessus.

Ensuite, on prolongera ce calcul en levant l’hypothèse.

Trois anniversaires, 24 personnes – Avec hypothèse
Probabilité de deux avec anniversaires différents : Pour le 1^er: 1 parmi 365 Pour le 2^e : 1 parmi 364 Pour le 3^e : 1 parmi 363 Pour le 4^e : 1 parmi 362 Etc.
Probabilité de deux anniversaires exactement à la même date : On a 2 choix parmi 24 pour ces deux individus, soit 276 possibilités. Ces deux ont un anniversaire parmi les 365 dates (resteront 364 dates), les deux autres doivent avoir des anniversaires différents. La quatité de cas possible est 365^24.
Probabilité pour que trois personnes parmi quatre aient le même jour anniversaire parmi cinq dates avec notre hypothèse : une seule paire de même anniversaire. La levée de l’hypothèse va réduire fortement cette probabilité.	Soit : 16 % ou 1/6

Trois anniversaires, 24 personnes – Sans hypothèse
Le calcul doit prendre en compte le cas des paires simultanées . Soit la revue suivante : Aucun anniversaire commun ; Une paire d’anniversaire commun ; Deux paires d’anniversaires commun, mais différents ; Trois … … 12 paires ont des anniversaires différents ; et Trois ou plus partagent la même date d’annivesaire.		Exemple Paul et Pierre: le 2 janvier Jacques et Simon: le 14 février Alors si Grégory est né le 2 janvier, nous avons notre triplé ; mais, cest également le cas si Guy est né le 14 février.
Aucun anniversaire commun sur 24 personnes.
Une seule paire de même anniversaire exactement.
Deux paires d’anniversaires communs, mais à des jours différents.  Choix de deux anniversiares pour les deux paires C(365, 2) ; Choix de deux personnes pour la première paire C(24,2) Choix de deux personnes pour la deuxième paire C(22,2) Prendre les autres tous différents: A(365-2, 24-4) = A(363, 20)	Rappel : arrangement de 20 parmi 363 :
Il faut recommencer ce calul pour 3 paires, pour 4, pour k jusqu’à 24/2 = 12. Formule générique en fonction de k:
Il est possible de simplifier :
Tous calculs fait (Calculette ou, mieux, tableur): Autre valeur pour 30 personnes.	P3 anniversaires au moins parmi 24 = 1,448 % P3 anniversaires au moins parmi 30 = 2,853 %

Suite	Calcul anniversaire avec le principe des tiroirs Amis Anniversaire le même jour de la semaine Coïncidences
Voir	Aïeuls Dates de naissance produit Dates de naissance en carrés magiques Dénombrement Jeux avec les âges Oncles Paradoxes Probabilités
DicoNombre	Nombre 0,5 Nombre 24 Nombre 87
Sites	Three Share a Birthday – Ask Dr. Math – Dr Rick et Dr Anthony – Ma page est largement inspirée de leurs propositions Three Birthdays On The Same Day – Jack’s Personal Blog on mathematics Probability of 3 people in a room of 30 having the same birthday – Mathematics (forum) The Three Birthday Problem – The Blog of Dr. Moron – On y trouve un graphe pour jusqu’à six anniversaires. Probability of 3 people in a room of 30 having the same birthday – Forum – Exposé du calcul avec Loi de Poisson Birthday Probabilities Calculator – dCode – Notez que le résultat du calcul est sur la colonne de gauche Exact Solutions of the Generalized Birthday Problem
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Probabil/Anniver3.htm