NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 08/04/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	NOMBRES ET JEUX
Débutants Général	Jeux avec Nombres						Glossaire Général
INDEX Jeux de nombres Jeux et énigmes Somme des chiffres Narcissiques Formes et motifs Nombres en chiffres Chiffres	Sudoku	Fubuko^®		Somme 100		Somme	Produit
	Bento		Kakuro		Somme 100 en 6 chiffres
			Sommaire de cette page >>> Nombres n = k fois le produit de ses chiffres >>> Produit des chiffres en cascade >>> Même produit des chiffres

PRODUIT des chiffres des nombres

Analyse du produit des chiffres d'un nombre. Un cas classique consiste à trouver les nombres égaux au produit de ses chiffres ou à un multiple comme cet exemple avec 175.

Quels sont les nombres ayant le même produit de leurs chiffres ?

Una autre application consiste à reformuler le produit des chiffres jusqu'à atteindre un seul chiffre. C'est la racine multiplicative du nombre.

Voir Brève 231 / Racine additive

Devinette

Complétez: 77, 49, 36, 18, ?

Réponse

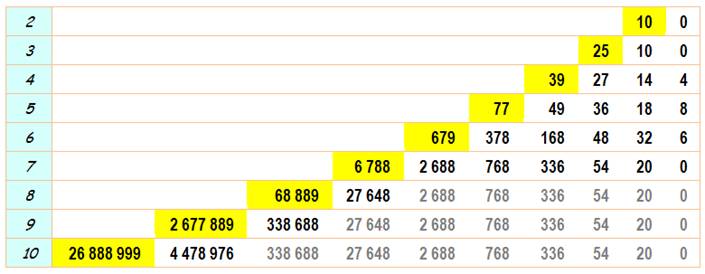
Record du produit des chiffres de 10 à 10 000

Le nombre 9999 détient le record jusqu'à 10 000 avec un produit égale à 6561 = 9^4. Le suivant est 25 999 avec le produit 7290.

[11, 1], [12, 2], [13, 3], [14, 4], [15, 5], [16, 6], [17, 7], [18, 8], [19, 9], [25, 10], [26, 12], [27, 14], [28, 16], [29, 18], [37, 21], [38, 24], [39, 27], [47, 28], [48, 32], [49, 36], [58, 40], [59, 45], [68, 48], [69, 54], [78, 56], [79, 63], [88, 64], [89, 72], [99, 81], [259, 90], [268, 96], [269, 108], [278, 112], [279, 126], [288, 128], [289, 144], [299, 162], [378, 168], [379, 189], [388, 192], [389, 216], [399, 243], [479, 252], [488, 256], [489, 288], [499, 324], [589, 360], [599, 405], [689, 432], [699, 486], [789, 504], [799, 567], [889, 576], [899, 648], [999, 729], [2599, 810], [2689, 864], [2699, 972], [2789, 1008], [2799, 1134], [2889, 1152], [2899, 1296], [2999, 1458], [3789, 1512], [3799, 1701], [3889, 1728], [3899, 1944], [3999, 2187], [4799, 2268], [4889, 2304], [4899, 2592], [4999, 2916], [5899, 3240], [5999, 3645], [6899, 3888], [6999, 4374], [7899, 4536], [7999, 5103], [8899, 5184], [8999, 5832], [9999, 6561].

Propriété

La puissance k de 9 détient le record des plus grands produits des chiffres des nombres de k chiffres.

Nombres n = k fois le produit de ses chiffres
Tous les cas jusqu'à n = 1000, hors cas triviaux comme 5 = 5 x 1. Ils sont 25. Exemple 816 => (8 x 1 x 6) x 17	n, P, k 11, 1, 11 12, 2, 6 15, 5, 3 24, 8, 3 36, 18, 2 111, 1, 111 112, 2, 56 115, 5, 23	128, 16, 8 132, 6, 22 135, 15, 9 144, 16, 9 175, 35, 5 212, 4, 53 216, 12, 18 224, 16, 14 312, 6, 52	315, 15, 21 384, 96, 4 432, 24, 18 612, 12, 51 624, 48, 13 672, 84, 8 735, 105, 7 816, 48, 17
Même chose pour les nombres de 1 000 à 10 000. Ils sont 39.	1112, 2, 556 1113, 3, 371 1115, 5, 223 1116, 6, 186 1131, 3, 377 1176, 42, 28 1184, 32, 37 1197, 63, 19 1212, 4, 303 1296, 108, 12 1311, 3, 437 1332, 18, 74 1344, 48, 28	1416, 24, 59 1575, 175, 9 1715, 35, 49 2112, 4, 528 2144, 32, 67 2232, 24, 93 2916, 108, 27 3111, 3, 1037 3132, 18, 174 3168, 144, 22 3171, 21, 151 3276, 252, 13 3312, 18, 184	3915, 135, 29 4112, 8, 514 4224, 64, 66 4416, 96, 46 6144, 96, 64 6624, 288, 23 6912, 108, 64 7112, 14, 508 7119, 63, 113 8112, 16, 507 8832, 384, 23 9315, 135, 69 9612, 108, 89

Produit des chiffres en cascade
Prenons un nombre à deux chiffes et multiplions ces deux chiffres. Si le produit est à deux chiffres, on poursuit l'opération. Quels sont les produits finaux possibles? Quelle est la chaine la plus longue?	24 2 x 4 = 8 25 2 x 5 = 10 1 x 0 = 0 26 2 x 6 = 12 1 x 2 = 2
Table des produits de 11 jusqu'à 102, ordonnés par résultats croissants Chaine la plus longue pour un nombre à deux chiffres Records Exploration jusqu'à 10 millions. Un autre exemple à 10: 126 888 999, normal le 1 initial ne change pas le produit. D'ailleurs, la propriété reste inchangée même avec un autre nombre que 1 placé en tête.

Voir Persistance multiplicative /Table des nombres égaux à k fois le produit de leurs chiffres

Même produit des chiffres

Combien y a-t-il de nombres dont le produit des chiffres, le 1 étant exclu, vaut 1 225 ?

Solution
Factorisation de 1225 = 5 x 245 = 5 x 5 x 49 = 5 x 5 x 7 x 7.

Si le produit vaut 1 255, ses facteurs à un seul chiffre valent 5, 5, 7, 7.

Ce sont les six nombres avec permutation de ces chiffres:

5 577, 5 757, 5 775, 7 755, 7 575, 7 557.

En introduisant le chiffre1, il existe une infinité de solutions comme:

15577, 115577 …

Autre exemple

Prenons le nombre 30 = 2 x 3 x 5. Ils sont huit nombres avec un produit de 30, le chiffre 1 exclu: 56, 65, 235, 253, 325, 352, 523 et 532.

Liste jusqu'à 50

Produit, (facteurs), quantité, [Nombres]

Exemple: 6, ses facteurs 2 et 3, trois nombres dont le produit est 6: 6, 23 et 32

Les nombres non mentionnées ne se sont jamais atteints par un produit de chiffres (dont, évidemment, les nombres premiers).

Records de quantité

Produit, quantité, [Nombres]

Au-delà on donne le produit atteint, ses facteurs et la quantité de nombres qui l'atteignent

Produit	Facteurs	Qté
2	2	1
4	2^2	2
6	2 × 3	3
8	2^3	4
12	2^2 × 3	7
24	2^3 × 3	16
36	2^2 × 3^2	21
48	2^4 × 3	32
72	2^3 × 3^2	47
96	2^5 × 3	51
144	2^4 × 3^2	78
240	2^4 × 3 × 5	84
288	2^5 × 3^2	150
360	2^3 × 3^2 × 5	159
432	2^4 × 3^3	227
576	2^6 × 3^2	275
720	2^4 × 3^2 × 5	348
864	2^5 × 3^3	397
1 440	2^5 × 3^2 × 5	456
1 728	2^6 × 3^3	480
2 520	2^3 × 3^2 × 5 × 7	492
2 592	2^5 × 3^4	639
2 880	2^6 × 3^2 × 5	785
…

Suite	Somme et produit des chiffres Nombre = S x P Nombres de Harshad Nombre de Harshad, somme et produit Somme-Produit des chiffres – Index
Voir	Jeux avec les chiffres Puzzles - Index
DicoNombre	Nombre 45 Nombre 77 Nombre 679 Nombre 6 788
Cette page	http://villemin.gerard.free.fr/aJeux/jeumcduM.htm