|
||||||||||||||||||||||||||||
![]()
|
Produit des chiffres d'un nombre Multant & Persistance multiplicative La somme des chiffres (racine
(additive) numérique) est utilisée pour effectuer la preuve par neuf.
Est-ce que le produit des
chiffres a une telle utilité? Non! Mais, son exploration est un bon amusement pour les
élèves de primaire et un terrain propice à des exercices de programmation en
secondaire. Un sujet également de passion pour les
mathématiciens-informaticiens qui veulent établir des records. Certains (comme le Kangourou des mathématiques), nomme
ce produit Multant. Son vrai nom est: racine multiplicative du nombre. |
Anglais: Digit-Product / Multiplicative
Persistence / Multiplicative Digital Root
|
Les chiffres d'un nombre sont itérativement multipliés
entre eux, et cela jusqu'à obtenir un seul chiffre. Les variantes consistent
à ignorer le chiffre zéro ou encore à considérer le produit des puissances
des chiffres. Dans le cas classique, on conjecture que la quantité
d'itérations ne dépasse pas 11 et le plus petit tel nombre est 277 777 788
888 899. Les nombres peuvent être regroupés en famille: toutes
les permutations du nombre (24 et 42 ont même produit) et tous les nombres
dont les chiffres forment un produit inférieur à 10 (6 et 23 ont même
produit; 6 est la forme compactée de 23). Il est possible d'optimiser les recherches de records
en sachant que tous les produits avant compactage sont de la forme: 2a3b5c7d. |
|
|
||
|
Avec la preuve par neuf, on
additionne les chiffres du nombre et on recommence pour aboutir à un seul
chiffre. Ici, on opère de la même manière mais avec la multiplication. Le multant
de 77 est le nombre final à un chiffre (8) et sa persistance
multiplicative est de 4 cycles. Tous les nombres ayant les mêmes
chiffes ont le même multant: 123 231 Les chiffres peuvent se multiplier et
donner le même multant: 123 16 |
Exemple Persistance multiplicative des nombres de 11 à 99 |
|
The persistence of a
number is the number of times you need to multiply the digits together before
reaching a single digit.
|
|
||
|
10 100
25 45 On note: 45, 20, 0 en faisant la multiplication
mentalement
69, 54, 20, 0 87, 56, 30, 0 9977, 3969, 1458, 0 (Inutile
de poursuivre les calculs) 9876, 3024, 0
de 0 à 10 2 (0 et 10) de 0 à 100 26 (0, 10, 20, 25, 30…) de 0 à 1000 478 de 0 à 10 000 6 741 |
Table pour début et fin
des nombres de 0 à 10 000 Pm: persistance multiplicative (quantité de cycles)
|
|
|
|
||
|
Ces nombres sont rares. Il faut en
effet maintenir le produit à 1. Avec 1 x 1 c'est possible, mais avec 9 x 9 =
81 nous voilà relancé à plus grand que 1. De sorte que jusqu'à 10 000, il n'y
a que 4 tels cas. Et, ce sont les repunits: |
1, 11, 111, 1111 … |
|
|
|
||
|
Les produits ne sont que très
rarement terminés par 3
ou 7. Nous ne serons pas étonnés de
retrouver peu de multants dans cette catégorie. Dix de chaque jusqu'à 10 000. Observez que pour n chiffres, il
s'agit toujours du même avec permutation des chiffres. |
|
|
|
|
||
|
Jusqu'à 10 000, ils ne sont que 20. Ce sont les cas où l'on trouve des 9
ou alors des 3,3, accompagnés de 1. |
|
|
|
|
||
|
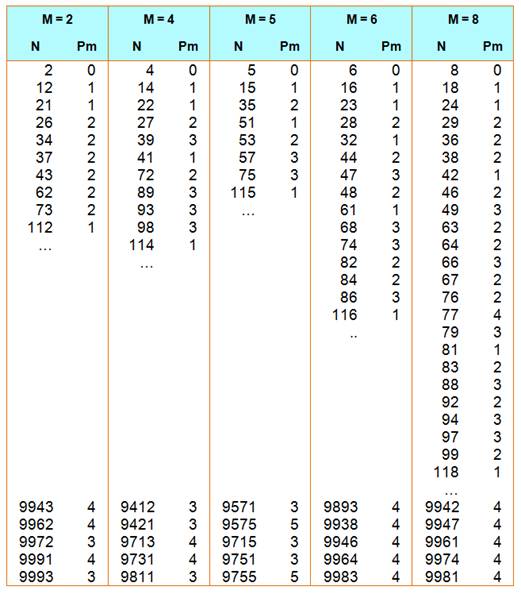
Ils sont très nombreux avec ces chiffres. Voici le début et la fin du tableau pour chacun de ces
chiffres, jusqu'à 10 000. |
|
|
Bilan:
quantité de multant selon le chiffre obtenu (jusqu'à 10 000)

![]()
Niveau avancé
|
Suite en Puzzle 341.
Multiplicative persistence, Erdos style – The prime puzzles &
problems connection – Carlos Rivera – Liste des calculs et code
Python pour ce record. |
Merci aux auteurs de m'avoir signalé
ce résultat
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
Quels
sont les plus petits nombres pour une persistance croissante 1, 2, 3 …? Exemple 679 => 378 => 168 => 48 => 32 => 6 Persistance multiplicative (pm) = 5 Multant (M): 6 Cas des nombres premiers Dans l'ordre les plus petits premiers sont: 11, 29, 47, 277, 769, 8
867, 186 889, 2 678 789, 26 899 889, 3 778 888 999, 277 777 788 888 989. |
Plus petit nombre pour les persistances
croissantes
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Conjecture Infirmée Voir
record ci-dessus |
La plus
grande persistance multiplicative connue est 11. On
conjecture qu'il n'y en a pas de plus grande. Le plus
petit nombre avec 11 est: 277 777 788 888 899
Pour la
persistance ce nombre est équivalent à: 277
777 788 888 899 =>
22222222222222222223333777777 ou
compactés: 21768692
=> 2193476 Yves Roques en propose un plus grand: 27 777 789 999 999 999 27 777 789 999 999 999 937 638 166 841 712 438 939 648 4 478 976 338 688 27 648 2 688 768 336 54 20 0 |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Sans le 1 |
On conjecture que, pour une
persistance multiplicative supérieure à 2, il existe un nombre maximum sans
le chiffre 1. Le plus grand nombre avec pm = 11 ne comportant aucun 1 serait
(conjecture): 7634219
=
77 777 733 332 222 222 222 222 222 222 = 7,77 … 1028 |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Base |
En base
2, la persistance multiplicative maximale est 2. En base 3, ce serait 3 (conjecture). On aurait ainsi selon la base
croissante: 2, 3, 3, 6, 5, 8, 6, 7 et 11 pour la base 10 |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Exploration |
On sait qu'il n'existe pas de persistance
multiplicative supérieure à 11 jusqu'à 1020 000 (Benjamin
Chaffin). La recherche de nombres plus grands
ou de nombres avec pm supérieures à 11 nécessite de travailler sur de très
grands nombres. Une exploration systématique est hors de portée de nos
ordinateurs de bureau. Quelles sont les pistes pour réduire
les recherches ? La vidéo d'Yves Roques développe une
piste de recherche. Parmi les pistes évidentes:
Une piste moins évidente mais très
payante:
Bilan pour le plus petit nombre de
PM donnée:
|
|
|
|||
|
Avec le
carré |
123 1² x 2² x 3² = 36 3² x 6² = 324 3² x 2² x 4² = 576 5² x 7² x 6² = 44 100 0 |
123 2-multant = 0 2-pm = 5 |
|
|
Avec le
cube |
123 13 x 23 x 33 = 216 23 x 13 x 63 = 1 728 13 x 73 x 23 x 83 = 1 404
928 0 |
123 3-multant = 0 3-pm = 4 |
|
|
Avec le
bicarré |
123 14 x 24 x 34 = 1 296 14 x 24 x 94 x 64 = 136
048 896 0 |
123 4-multant = 0 4-pm = 3 |
|
|
|
||
|
Erdos
propose d'ignorer les 0 s'ils existent et de poursuivre les itérations. Dans ces
conditions, la persistance multiplicative dépasse 11. Voir le développement
ci-contre 74282914
à une persistance de 13. |
55555555555555557777777777777 14784089722747802734375 49962386718720 438939648 4478976 338688 27648 2688 768 336 54 20 2 Bilan, 2, 12 |
|
![]()
Programmation
|
Les
programmes Maple et Python proposés calculent la persistance multiplicative
d'un nombre.
Voir
les sites proposés pour ceux qui voudraient optimiser les
programmes et se lancer à la poursuite des records. (1020 000 en
2019). |
|
|
|||
|
|
|
Commentaires La première procédure (pme) calcule le produit des chiffres d'un
nombre. Le nombre n est convertit en
base 10 pour disposer de la liste des chiffres. Avec mul, on multiplie les chiffres successifs de N jusqu'à nop(n) qui donne la quantité de chiffres. On en profite pour imprimer
le produit. La procédure suivante
procède à l'itération du calcul du produit jusqu'à obtenir un seul chiffre
(tant que R est supérieur à 9). La variable kt
compte la quantité d'itérations. Le programme principal fait
appel à ces procédures avec le nombre n indiqué. Résultat en bleu avec le
nombre, suivi des calculs intermédiaires et en fin le bilan avec le multant
(0) et la persistance multiplicative (11). |
|
Voir Programmation – Index
|
|
|||
|
|
|
Commentaires La fonction pm calcule la persistance multiplicative de n en
utilisant une méthode récursive (appel
du programme à lui-même) Le programme va traiter les
caractères (string) des nombres et les
transformer en chiffres (int) Pour commencer, on crée un
critère d'arrêt avec une longueur de chaine = 1. La variable chiffres contient la liste des caractères
transformés en chiffres. La variable M contient les multants successifs. Ils sont
imprimés. La procédure est relancée en
prenant le multant comme nouveau nombre à traiter. En donnant à n la valeur
indiquée, on appelle la fonction; le résultat est la liste en bleu. |
|
Voir Programmation
Python
![]()
|
Suite |
|
|
Voir |
|
|
|
|
|
Cette page |
http://villemin.gerard.free.fr/aNombre/MOTIF/Chiffres/Multant.htm |
![]()