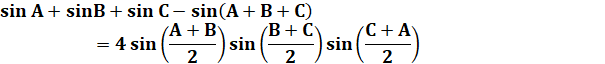|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
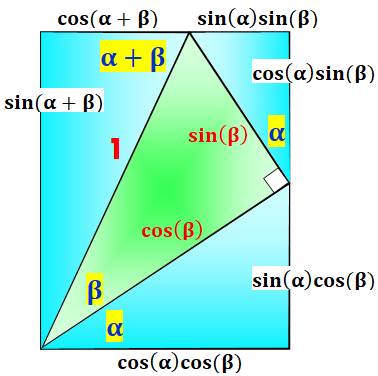
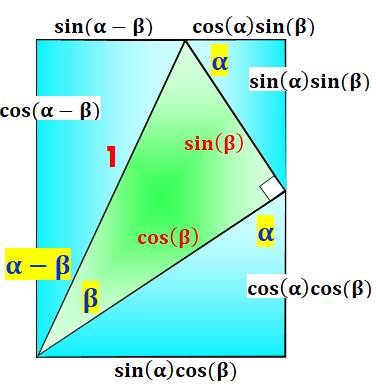
IDENTITÉS TRIGONOMÉTRIQUES Addition des angles |
Quelques relations en images
|
|
|
|
|
Pour entre 0° et 90° |
|
|
Note:
les valeurs indiquées résultent simplement de la lecture des sinus et cosinus
des angles selon
la valeur de l'hypoténuse (aucun calcul).
Les relations
indiquées témoignent de l'égalité deux à deux des côtés du rectangle.
|
|
|||
|
Sinus |
sin (A + B) sin (A –
B) sin (B –
A) |
= sin A . cos B + cos A . sin B = sin A . cos B – cos
A . sin B = – sin (A – B) Voir Démo |
|
|
Cosinus |
cos (A + B) cos (A –
B) cos (B –
A) |
= cos A . cos B – sin
A . sin B = cos A . cos B + sin A . sin B = cos (A – B) |
|
|
En abrégé |
sin (A+B) cos(A +B) sin(A+B+C) cos(A+B+C) sin(A+B+C+D) cos(A+B+C+D) |
=
sc+cs =
cc-ss =
scc-sss+csc+ccs =
ccc-css-ssc-scs = sccc-scss-sssc-sscs+cscc-csss+ccsc+cccs =
cccc-ccss-cssc-cscs-sscc+ssss-scsc-sccs |
|
|
Produits |
sin (A + B) . sin (A – B) |
= sin² A – sin² B = cos²B – cos² A |
|
|
|
cos (A + B) . cos (A – B) |
= cos² A – sin² B = cos²B – sin² A |
|
|
Tangente |
tan (A + B) |
|
|
|
tan (A – B) |
|
|
Cotangente |
cot (A + B) |
|
|
|
cot (A – B) |
|
|
Arc |
arcsin A |
|
|
|
arccos A |
|
|
|
arctan A |
|
|
|
arccotg A |
|
|
Atan2 |
atan2 (
|
|
|
Trois
angles |
tan (A + B + C) |
|
|
|
0 |
Voir Démo |
Voir Multiplication de
nombres complexes
|
Il
est possible de transformer cette somme en un seul cosinus. On
pose A et B en termes de lignes trigonométriques comme suit.
|
Voir Application
à la résolution d'une équation
|
|
|||
|
Formules de Prosthaphaeresis ou de Simpson |
|||
|
Sinus |
sin A + sin B |
= 2 sin
½ (A + B) . cos ½ (A – B) Voir Démo |
|
|
|
sin A – sin B |
= 2
sin ½ (A – B) . cos ½ (A + B) |
|
|
Cosinus |
cos A + cos B |
= 2
cos ½ (A + B) . cos ½ (A – B) |
|
|
|
cos A – cos B |
= 2 sin ½ (B – A)
. sin ½ (A + B) = – 2 sin ½ (A – B) .
sin ½ (A + B) |
|
|
Tangente |
tan A + tan A tan A – tan B |
= sin
(A + B) / cos A . cos B = sin
(A – B) / cos A . cos B |
|
|
Spéciale |
|
||
|
Dans le triangle |
Voir Démo |
||
|
|
|||
|
Sinus et
cosinus |
2 sin A . sin B 2 cos A . cos B |
= cos
(A – B) – cos (A + B) = cos
(A – B) + cos (A + B) |
|
|
|
2 sin A . cos B 2 cos A . sin B |
=
sin (A + B) + sin (A – B) =
sin (A + B) – sin (A – B) |
|
Voir Application au
triangle isocèle / Multiplication avec ces
identités (Prosthaphaeresis)
![]()
Toutes les expressions de sommes d'angles



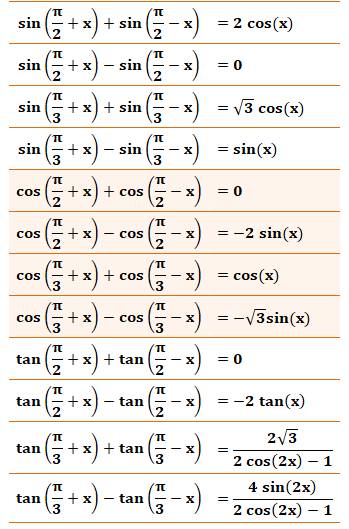
Voir Brève
770 – Méthode de calcul de ces
expressions
Voir Comment calculer ces expressions
avec Maple
Sommes avec angle et un
multiple

Voir Calculs avec ce type d'expressions
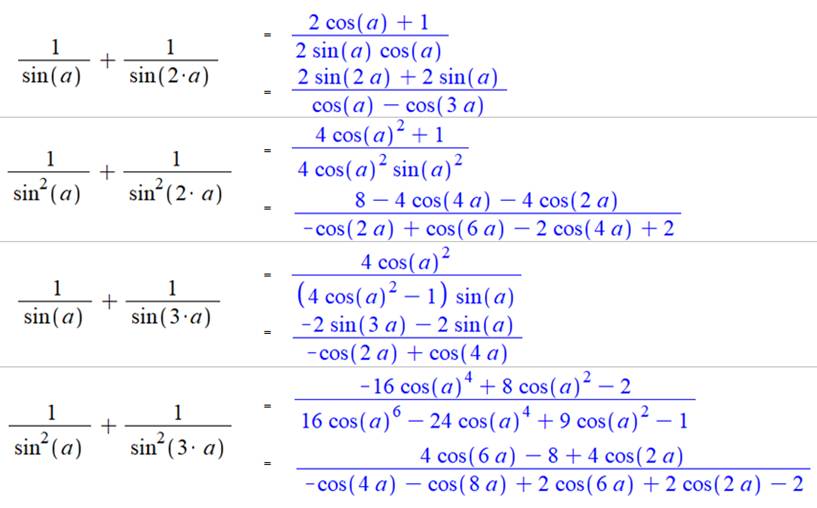
![]()
|
Bases |
|
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/aMaths/Trigonom/aaaBases/Reladdit.htm
|
![]()