|
|||||||||||||||||||||||||||
![]()
|
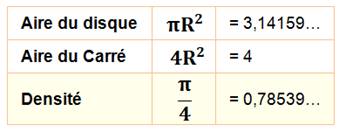
Densité des arrangements de disques Problème équivalent à l'empilement des sphères, traité
ici en deux dimensions. Sur cette page nous donnons quelques indications de
calculs des aires et des densités. Nous présenterons enfin la preuve de la
densité minimale. |
|
|
||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Nous constatons sur la figure avec les trois cercles
tangents (plus haut) que l'angle théta vaut alors 60° = Pi / 3. C'est la
valeur maximale pour l'angle théta. |
|
|
|
La fonction est croissante et son maximum est justement
atteint pour Pi/3.
Conclusion, cette configuation de cercles tangents est bien
la plus dense. |
|
Voir Identités
trigonométriques / Aire du secteur
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Cercle/aaaAIRE/Densite.htm
|
![]()