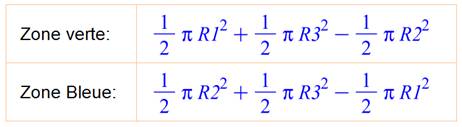|
||||||||||||||||||||||||||||||||||||
![]()
|
CROISSANT
|
Anglais: Crescent
|
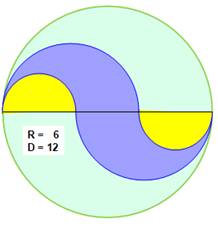
Problème (simple
!) Trois demi-cercles: petit, moyen et grand. La figure doublée donne
cette figure. Aire la zone bleue ? Application numérique avec le rayon du grand
cercle: R = 6 cm. Piste Les diamètres successifs sont dans les rapports 1/2,
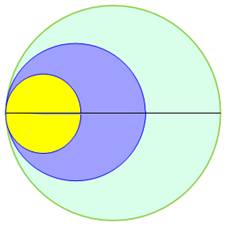
2/3 et 1. La figure de droite montre l'astuce pour
faciliter le calcul: translater
les demi-cercles du bas. |
|
|
|
Calcul
|
||
Voir Défis géométriques
|
|
|
|
A =
|
|
|
|
|
|
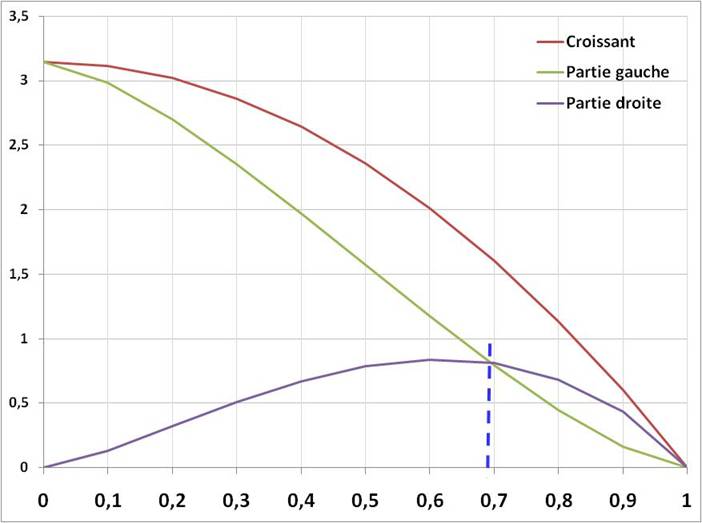
cos Application
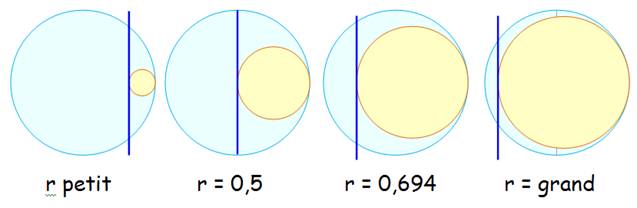
numérique Avec R = 1 et r
de 0 à 1 en abscisse.
Pour r = 0,6943239332500 … la partie gauche du
croissant à la même aire que la partie droite. Dans cette configuration C est le centre de gravité
du croissant. Note
r =
0,618033988 A =
1,941611038 A1 =
1,103082983 A2 =
0,838528055 Écart = 0,264554927 |
|
|
|
|||
|
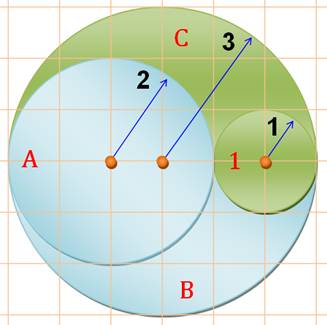
Problème Trois
cercles de rayon 1, 2 et 3 selon la figure. Quelle est l'aire du
"croissant" vert? Et celle de la zone bleue? Solution Si l'aire du disque de rayon 1 vaut 1 unité
d'aire. L'aire du disque de rayon 2 (A) est quatre fois plus grande (l'aire
croît comme le carré du rayon). Et l'aire du grand disque vaut 9. Selon la géométrie du dessin les aires B et
C sont égale. En remplaçant, nous trouvons que l'aire de
B ou de C = 2. Verte et bleue: l'une est le double de
l'autre en superficie. Aire bleue
= 2 x Aire verte. |
A = 4 Aire grand disque = 1 + A + B + C = 9 = 1 + 4 + 2B = 9 2B = 4 B = C = 2 Aire de zone verte: 1 + C = 1 + 2 = 3 Aire de zone bleue: A + B = 4 + 2 = 6 |
||
|
Formules générales |
|
||
|
|
||
|
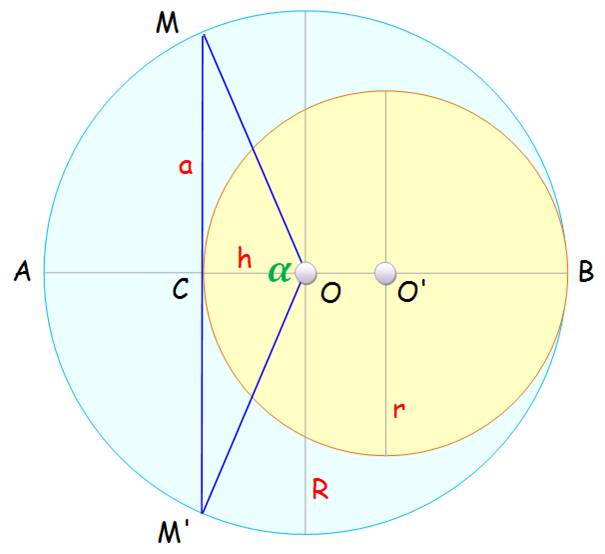
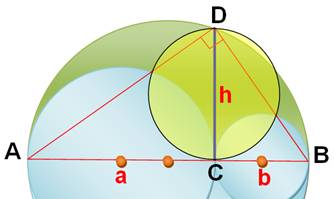
Problème Trois
cercles disposés comme sur la figure. La zone verte est appelée arbelos (ou
tranchet de cordonnier). Quelle est son aire? Archimède a montré qu'elle est
égale à celle du disque de diamètre h. Solution L'astuce
repose sur la relation à établir dans le triangle rectangle
ADB. En effet, on sait que: h² = ab En
remplaçant ab pas h² dans l'évaluation de l'aire de
l'arbelos, on retrouve l'aire du disque de diamètre CD. Attention L'aire d'un disque
est Il
existe deux arbelos: en haut et en bas, d'où la division par 2. |
Aire disque AC = Aire disque CB = Aire disque AB = Aire arbelos: =
= = = aire disque CD |
|
Voir Arbelos
multiple résolu par inversion – Chaine de Pappus / Sangakus
Cercles
jumeaux d'Archimède / Aire de découpes dans le cercle
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Cercle/aaaAIRE/Croissan.htm |
![]()