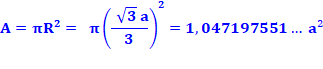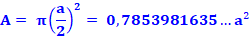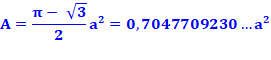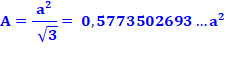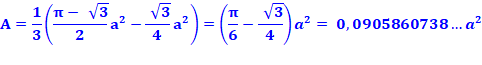|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
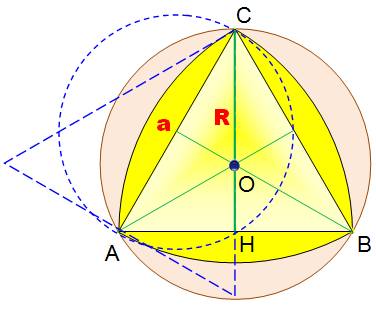
TRIANGLE
de REULEAUX Triangle équilatéral flanqués de segments
de cercles. Sur chaque côté, on dessine
le segment de cercle avec le sommet opposé comme centre et la longueur du
côté comme rayon. Propriété: le triangle de Reuleaux est une figure à largeur constante
(tous les diamètres ont la même longueur). Parmi les courbes d'égale
longueur, cette courbe de Reuleaux est celle qui présente l'aire minimale
(Théorème de Blaschke et Lebesgue). Applications: moteurs rotatifs;
plaques d'égout ne pouvant pas tomber dans le Franz Reuleaux (1829-1905)
ingénieur et technologue allemand. |

Le périmètre est celui du
demi-cercle.
|
|
||
|
Aire
cercle rose (diamètre R)
Aire
cercle bleu (diamètre a)
Aire du
triangle de Reuleaux (côté a)
Aire du
triangle équilatéral bleu (hauteur a)
Aire du triangle
équilatéral (côté a)
|
|
|
|
Aire d'un
segment jaune
|
||
|
En
2013, H.L Resnikoff a prouvé que la densité
d'une certaine manière d'arranger les triangles de Reuleaux atteignait 0,923,
dépassant la compacité
des cercles (0,9069…). Il conjecture
qu'il s'agit de la densité maximale.
|
Source: On curves ans surface of constant
width – H.L. Resnikoff
|
|
||
|
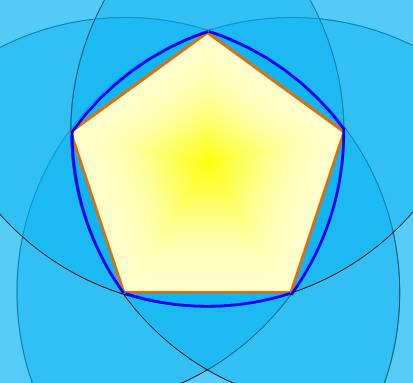
Tous les
polygones réguliers avec un nombre impair de
côtés peuvent être transformés en polygones de Reuleaux. L'arc de
cercle apposé à un côté est centré sur le sommet opposé. Illustration
avec le pentagone
régulier |
|
|
|
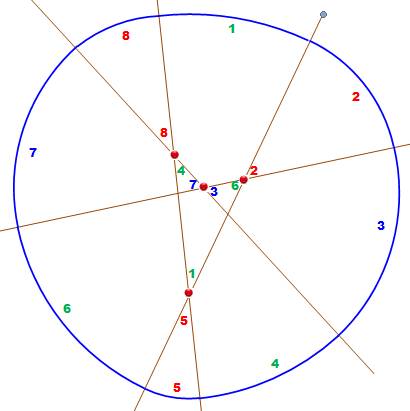
Il est
possible de construire une figure de Reuleaux – une
figure à largeur constante – à partir d'une série de droites sécantes,
en choisissant bien les centres des arcs de cercle. |
|
|
|
English corner |
|
|
In the 19thcentury the German engineer
Franz Reuleaux discovered a new type of triangle now referred to as a Reuleaux Triangle. It is constructed by drawing
an equilateral triangle of side-length s and then drawing three circles of
radius s each centered at the
three vertexes of the original triangle. The Reuleaux triangle is a constant width curve that is based on an
equilateral triangle, where all points on a side are equidistant from the
opposite vertex. This so-called equilateral curve-triangle is the simplest non-circular curve that has a constant
width, as proposed and analyzed by Franz Reuleaux. In general, any regular
polygon with an odd number of sides can be used as the basis for a Reuleaux polygon
of constant width. |
|
![]()
|
Retour |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Triangle/Types/Reuleaux.htm |
![]()