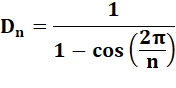|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Spirale Logarithmique & Le problème des quatre souris (chiens, tortues, souris…)
Quatre souris sont aux coins
d'un carré. Chacune en
poursuit une autre. Cette poursuite se termine au centre du carré et, les
trajets engendrent quatre spirales logarithmiques. Curieusement dans ce cas, la
distance parcourue par chaque souris est égale à la distance qu'aurait
parcouru la souris vers sa congénère immobile, soit la longueur du côté du
carré. Ce ne serait pas le cas avec cinq souris aux sommets d'un pentagone, ou tout autre polygone. Ce problème a été popularisé
par Martin Gardner dans sa rubrique "Mathematical Games" du
Scientific American (1965). |
Anglais: Four mice
(turtles, bugs, beetle, dogs …) problem
The four bug
cyclic pursuit problem
|
|
||
|
Courbe d'équation
polaire: Cette courbe
s'enroule de plus en près d'un point
central. Construction: une droite (rayon)
tournant uniformément autour d'un point O. Un point M sur cette droite qui se déplace
à une vitesse proportionnelle à OM. La spirale logarithmique est le lieu du
point M. L'angle polaire
croit de façon arithmétique, alors que le rayon vecteur croit de façon
géométrique. La longueur de ce rayon est multipliée par le nombre d'or chaque fois que sa
direction tourne d'un quart de tour. En phyllotaxie, les
spirales de développement des primordia sont logarithmiques. |
Courbe dont l'angle tangentiel polaire reste constant (tangente au
point de rencontre d'un rayon avec la courbe, en jaune). |
|
|
|
||
|
Une souris ou un insecte
(scarabée) ou une fourmi … à chaque sommet A, B, C et D du carré. Le scarabée A poursuit le
scarabée B, le B poursuit le C, le C le D et le D le A. L'illustration présente la
situation à des moments successifs discrets. En réalité les trajets en bleu
sont des courbes continues. Les scarabées finissent pas se rencontrer au centre du carré en ayant
parcouru chacun l'équivalent du côté du carré. |
Les quatre scarabées dans leurs poursuites respectives tracent quatre
spirales logarithmiques. |
|
|
|
|||
|
Situation en fin de première
étape: les quatre bestioles sont toujours au sommet d'un carré (cf. les quatre triangles rectangles sur les bords sont égaux …). Faisons pivoter ce carré
pour le remettre "droit" comme celui d'origine. Calons ce carré sur le
sommet B (tracé en pointillés verts). Le scarabée progresse de
deux carreaux (D) à chaque étape (flèche bleue et verte pour A). En fin de première étape, le
carré vert est égal à l'original diminué de D. Cette opération se répète à
chaque étape: redressement du carré et calage en B, avec réduction du côté de
D. Le scarabée A atteindra son
but lorsque le dernier carré deviendra un point, c'est-à-dire lorsque le
scarabée aura parcouru l'intégralité de la distance AB (sur l'illustration,
il faudra 10 étapes) |
Cette construction montre que la distance parcourue par chaque
scarabée est égale à la mesure du côté du carré. Une ligne bien courbe qui
égale en longueur un segment de droite! |
||
|
La distance parcourue pour un polygone à n côtés
Le tableau donne les valeurs
jusqu'à n = 10 (décagone). Pour n = 4, cosinus (Pi/2) vaut 0 et Dn
= 1. |
|
||
|
|
||
|
La mise en équation de la courbe de poursuite nécessite la
connaissance des dérivées et
des intégrales. Pour un carré de 10 de côté, l'équation polaire est la suivante:
L'équation d'une spirale logarithmique,
illustrée ci-contre avec la fonction F (en rouge) et –F (en vert). |
|
|
|
Autant,
la programmation n'est pas très
simple avec les langages informatiques déclaratifs classiques, autant, c'est
plus simple en langage LOGO.
(Appel à mes souvenirs des années 1980 …) Retrouvez
la programmation en Advanced Logo: A language for Learning
by Michael Friendly (e-book) |
Autres poursuite avec des polygones

Dessins extraits de Bugs on a square
by Gary Antonix
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()