NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 03/04/2021 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	CONSTANTES
Débutants Nombres	RACINE de 2 √2 = 1, 41 42 …			Glossaire Nombres
INDEX Puissance Décomposition Général	Introduction	Valeur	Propriétés	Géométrie
	Historique	Calcul	Irrationnel	Doubler
		Sommaire de cette page >>> Carré >>> Carré double >>> Avec le triangle rectangle >>> Cercle >>> Construction des racines de n >>> Escargot de Pythagore >>> Construction 2 >>> Construction directe de racine de n

Géométrie et racine de 2

& Construction de racine de n

CARRÉ
Diagonale du carré de côté unité Théorème de Pythagore: D² = 1² + 1² = 2 et D = √2 Et, d'une manière générale: D = a . √2 Avec a la mesure du côté du carré	Le carré est découpé par sa diagonale en deux triangles rectangles isocèles
Côté du carré d'aire égale à 2 A = 2 = a² a = √2

CARRÉ DOUBLE
Carré double Le carré rouge comporte 4 triangles Le carré bleu en compte 2 de même taille Le grand a une aire double de celle du petit Longueur du côté du grand carré, diagonale du petit Aire grand carré = 2 fois aire du petit x . x = 2 x (1x1) x² = 2 x = 2 2 diagonale du carré de côté 1 Mieux! Pythagore va plus vite x² = 1² + 1² = 2	Notez que Doubler le côté du petit carré multiplierait son aire par 4 et non par 2. Prendre une moyenne (1+2)/2 ne convient pas non plus. Seule la valeur 2, non évidente a priori, fait l'affaire :

Suite	Dialogue sur la vertu de Platon et le doublement de l'aire du carré
Voir	Doubler l'aire du carré Doubler le volume du cube

Avec le triangle rectangle
Deux méthodes possibles avec un triangle rectangle: Avec le théorème de Pythagore, on a par exemple h² = 2² et l’hypoténuse vaut : Avec le théorème sur la hauteur : b = 3 et la hauteur vaut .

CERCLE
Dans le cercle de rayon 1 Soit le point M situé sur un rayon à 45°:	Les coordonnées de M sont: x = 2 / 2 y = 2 / 2 Ce sont les valeurs de: sin 45° = 2 / 2 cos 45° = 2 / 2

CONSTRUCTION des racines d'un nombre
Carré de côté unité. La diagonale est rabattue sur le côté horizontal. Mesure D² = 1² + 1² => D = 2 On élève la perpendiculaire, donnant naissance à un rectangle de côtés 1 et 2 La diagonale est rabattue sur le côté horizontal Mesure D² = 1² + (2)² => D = 3 Etc. Mesure D² = 1² + (3)² => D = 4 Pour racine de 5, la construction est particulièrement simple. Base du rectangle d'or.

Voir Construction géométrique des nombres / Autre construction / Construction de a², 1/a

Escargot de Pythagore
Sur le même principe, on peut aussi construire une spirale dite rectangulaire ou escargot de Pythagore. Autres noms: spirale de Théodore de Cyrène ou spirale d'Einstein En 1958, Erich Teuffel a démontré que les rayons ne se superposent jamais.
Construction avec GeoGebra Triangle rectangle isocèle ABC sur le carré (1, 1) du quadrillage. Suite de la construction expliquée pour le triangle ADE: Perpendiculaire en D à AD. Segment de longueur 1 à partir de D. Cercle avec ce rayon et centre D. Intersection en E avec la perpendiculaire. Segment AE qui vaut racine de 4 = 2. Remarquez que si AB = 1, alors AE vaut 2.
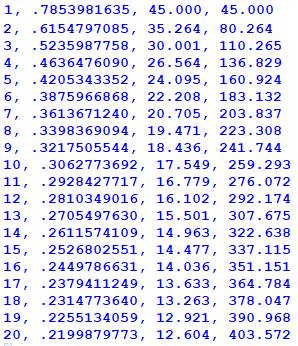
Mesures Valeur de l'angle n Tableau: n, angle en radian, angle en degré, et angle depuis l'origine.

Voir Autres constructions avec GeoGebra / Brève 616

CONSTRUCTION de √2
Construction RÈGLE ET COMPAS Segment de départ OA dont la mesure est 1. Prolonger à gauche dans la direction A'. Cercle de centre O et de rayon 0A. Il permet de marquer le point A'. Perpendiculaire à AA' en O (médiatrice); cercle de centre A d'ouverture r' quelconque; cercle de centre A' de même ouverture r'; Se coupe en O'. La médiatrice coupe le cercle en M. AM mesure 2. Démonstration Évidente. Diagonale du carré de côté 1.
Construction COMPAS SEUL Segment de départ OA dont la mesure est 1. Construction de la rosace classique (une demie suffit). Cercle de rayon OA. Report de ce rayon à partir de A pour créer B, puis B' et enfin A'. Construction de la médiatrice. Cercle centre A rayon AB'. Cercle centre A' rayon A'B = AB'. Le segment OM mesure 2. Démonstration Triangle A A' B' Rectangle en B, car inscrit dans un demi-cercle AB'² + A'B'² = AA'² AB'² = (2R)² - R² = 3R² = 3 Par construction: AM = AB' = √3 Triangle OAM: OM² = AM² – OA² OM² = 3 – 1² = 2	Figure particulière donnant la racine des trois premiers nombres 1, 2 et 3

Voir Construction

Construction directe de racine de n
Tout nombre est somme de quatre carrés. Prenons le nombre 15: 15 = 1² + 1² + 2² + 3² = a² + b² + c² + d² = u² + v² avec u² = a² + b² et v² = c² + d². Construction Placez un couple de valeur en abscisse de part et d'autre de l'origine (a et d, par exemple) L'autre couple sur l'axe des ordonnées. Les diagonales sont nommées u et v et leurs longueurs sont reportés sur les axes (arcs verts). Le segment (rose) qui joint les intersections avec les axes est notre racine (ici racine de 15) Justification

Simplification Cas d'une somme de trois carrés. Prenons le nombre 14: 14 = 1² + 2² + 3² = u² + c² + d² = u² + v² avec v² = c² + d². Construction Placez la valeur de u en ordonnées et la suite st identique. Justification

Quelques exemples

Deux carrés

Trois carrés

Quatre carrés

Voir Brève 530 / Racines de14 et de 15

Suite	Racine de 2 – Historique Doubler l'aire du carré Construction géométrique des nombres
Retour	Racine Racine carrée Développement de Taylor
Voir	Constructions géométriques élémentaires Imaginaires Constantes Pi Nombre d'Or
Diconombre	Nombre 2 Racine de 2
Livre	Le Fabuleux destin de racine carrée de 2 – Benoît Rittaud – 2006
Site	Spiral of Theodorus – Wikipedia
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Nombre/Rac2Geom.htm