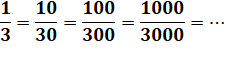|
||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
DIVISION avec des décimales Comment traiter les chiffres après la virgule. |
|||||
|
Je m'y connais déjà
un peu >>> Je suis tout nouveau
sur le sujet >>> |
Rappel
|
||||
Voir
Les quatre opérations – Junior / Système
décimal
|
|
||
|
|
Multiplier le dividende
par 10, multiplie le quotient par 10. Multiplier le diviseur par 10, divise le
quotient par 10. Logique, non? |
|
|
Cette logique d'apport de "0"
et cette mécanique de décalage de la virgule
sont celles qui sont utilisées pour calculer les divisions décimales des plus
simples aux plus complexes. |
||
|
Avec
des décimales au dividende |
|
|||||||||||||||||||||||||||||||||||||
|
Nous sommes 5. Combien chacun? Y
compris des morceaux de parts si nécessaire.
Nous
pouvons bien sûr transformer les euros en centimes: 4 euros donnent 400
centimes. Nous pouvons partager ces centimes. Autrement dit poursuivre la
division. Vous
trouverez rapidement que 400 divisé par 5 donne 80. Chacun peut recevoir 80
centimes d'euros en plus.
Simplement
en complétant le nombre à diviser avec des 0 fictifs, précédés d'une virgule (marque des nombres décimaux). La
division est poursuivie normalement en
mettant une virgule dans le diviseur dès que nous abaissons des zéros
derrière la virgule du nombre à diviser. |
En rose, la suite
de la division avec les décimales; on place alors une virgule dans le
quotient. Résultat: 12014 / 5
= 2402,8 Vérification: 2402,8 x
5 = 12014 |
|||||||||||||||||||||||||||||||||||||
Si
vous doutez, allez à la page débutant
|
Avec
des décimales aussi au diviseur |
|
||||||||||||||||||||||||||||||||||||||
|
La virgule du
diviseur est éliminée. Puis, on effectue la division comme indiqué ci-dessus.
0,001 = 1 x 10-3 à diviser par
5,213 & avec la
puissance de 10: => 0,2 10-3 |
Rappel
Exemple
Multiplication par 10 de chaque côté:
Multiplication par 100 de chaque côté:
Multiplication par 1000 de chaque côté:
|
||||||||||||||||||||||||||||||||||||||
|
Le diviseur est plus grand que le dividende |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Approche
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Division
posée normalement
68 devient
68,00000…
Commentaire
|
Résultat 68
/ 78 = 0,871794
871794 87… Nombre
périodique >>> |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
Exemple: 14 789 à diviser par
67 Prolonger avec une virgule
Cela ne change pas sa valeur, bien
naturellement 14 789 = 14 789, 0000…
Si nous poursuivons l'opération, la suite
sera formée de décimales Il est naturel de placer une virgule aussi
derrière le nombre entier obtenu pour le quotient 220 devient 220,
Une fois les deux virgules introduites, la
suite de l'opération s'effectue rigoureusement
-
soit le reste devient nul, -
soit le reste est toujours présent (non nul), |
|
Merci à Kevin Forget pour sa vigilance
|
Effectuons cette division en décimal
Le résult 14 789 / 67 = 220, 731
… En continu 14 789 / 67 = 220, 7313432835 8208955223
8805970149 2537313432 8358208955 2238805970 1492537313 4328358208 9552238805
9701492537 … |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Il s'agit
de calculs un peu plus longs. Il faut
surtout agir avec méthode et bien poser
les opérations.
Je note 1 à droite et retranche une quantité équivalente à
droite, soit 1 x 4321 = 4321. Il reste
1013
Avec le
reste précédent cela donne 10135.
Soit 2 x 4321 = 8642. Je note 2 au quotient (à droite)
et le reste 1493 à gauche.
Avant de
l'abaisser, je note que nous franchissons la virgule. Je signale le même franchissement de l'autre côté en
notant la virgule dans le
quotient.
C'est la
fin de la division. |
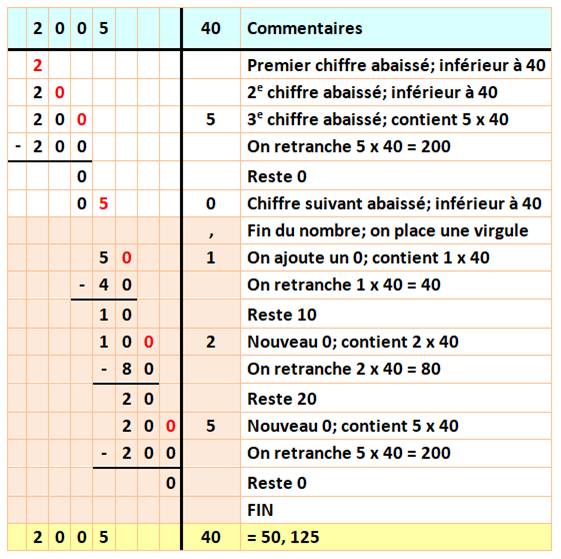
Résultat 53345,6785269
/ 4321 = 12, 456789 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Autre exemple
![]()
|
Retour |
|
|
Suite |
|
|
Retour
Voir
résumé en: Très
utile: |
|
|
Voir |
|
|
Cette page |