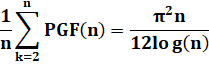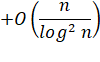NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 21/09/2019 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	DIVISION
Débutants Diviseurs	DIVISEURS					Glossaire Diviseur
INDEX Décomposition	Généralités		Calculs	Fact. Premiers	Liste
	2^n Diviseurs		Communs	Records
	Plus grand facteur			Théorie – Valeur, quantité, somme >>>
		Sommaire de cette page >>> Table des facteurs les plus grands des nombres de 2 à 159 >>> Somme des plus grands facteurs >>> Recherche du plus grand facteur – Pas à pas >>> Procédure de recherche du plus grand facteur >>> Plus grand facteur et racine de n

FACTEUR le plus grand d'un nombre

Table des plus grands facteurs et de leur somme. Les nombres rudes et les nombres mous selon la relation avec la racine de n.

Programmation pas à pas et établissement d'une procédure.

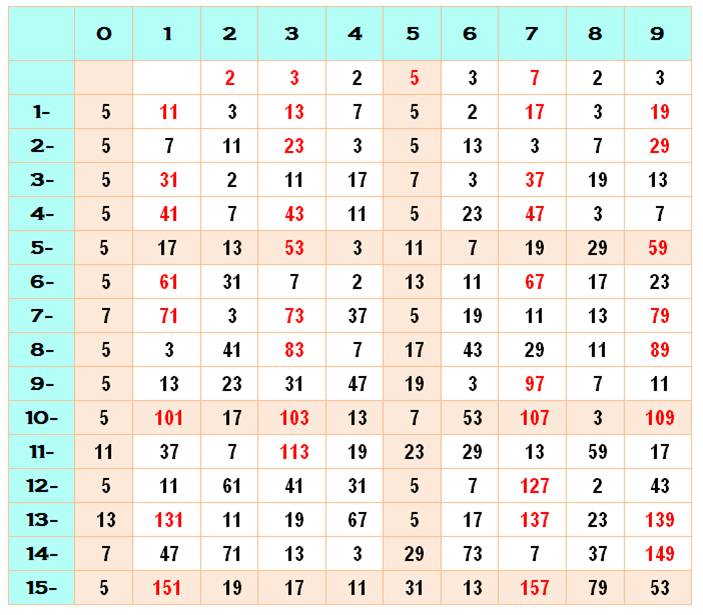
Table des facteurs les plus grands des nombres de 2 à 159
Exemple: ligne 2- et colonne 2 => 22 et son plus grand facteur est 11. En rouge, les nombres premiers dont le plus grand facteur est lui-même.

Voir Tables – Index

Somme des plus grands facteurs
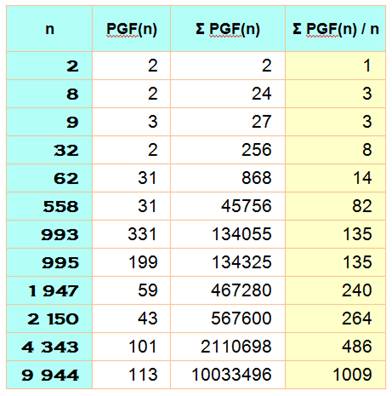
On calcule la somme de tous les facteurs les plus grands pour les nombres de 2 à n. Pour n = 5, on trouve les facteurs (2, 3, 2, 5) et leur somme est 12. Cette somme divisée par n = 5 donne: 2,4. Le second tableau montre toutes les valeurs de n pour lesquelles la somme des facteurs les plus grands est divisible par n. Erdös a calculé la valeur de la moyenne de cette somme:	Sommes pour n de 2 à 12 Sommes divisible pour n de 2 à 10 000

Recherche du plus grand facteur – Pas à pas Programmation avec Maple
	Définition d'un nombre n dont on connaît les facteurs (pour mieux apprécier la suite). On place les facteurs de n dans la mémoire nf. C'est une liste de deux termes: d'abord [1] qui signifie que le nombre est positif puis la liste des facteurs […], chacun avec sa valeur suivi de sa puissance. L'instruction op permet d'extraire des éléments dans la liste. L'élément 1 de nf est 1. L'élément 2 de nf est toute la liste des facteurs. Il est possible de l'appeler en prenant des indices négatifs (astuce!). L'élément -1 de la nf est également toute la liste des facteurs. Pour accéder au dernier élément [7,1] de la liste des facteurs, prenons le terme -1. Puis pour finalement obtenir le plus grand facteur 7, prenons le premier élément de ce dernier terme.
	En résumé Seules ces instructions suffisent pour extraire le plus grand facteur d'un nombre.

Voir Extraction des facteurs et calcul de la richesse d'un nombre

Procédure de recherche du plus grand facteur
Nous venons de voir comment extraire le plus grand facteur d'un nombre. Voyons comment en faire une procédure; c'est-à-dire une sorte de nouvelle instruction Maple.
	Appel au package de théorie des nombres. Définition de la procédure: Plus Grand Facteur (PGF). n est déclaré (::) comme positive integer (entier positif). Vérification que n est différent de 1. Calcul des facteurs. Extraction du plus grand facteur. % indique qu'il faut prendre le dernier résultat en mémoire. Fin de la procédure Appel de la procédure PGF pour le nombre indiqué; réponse 13. Appel répété (map) de la procédure pour la liste […] des nombres indiqués. Appel répété de la procédure pour la séquence (suite) des nombres de 10 à 20. Exemple de message d'erreur pour un appel avec le nombre 1.

Voir Procédure / Programmation – Index

Plus grand facteur et racine de n
On compare le plus grand facteur de n à la racine carrée de n. Si PGF > , le nombre est appelé "unusual number" par Greene et Knuth (1190), ou "rough number" ou "jagged number" par Finch (2001). Ils sont repérés par le type 1 dans le tableau ci-contre. Dans le cas contraire, ce sont des "smooth numbers". Source Greatest Prime Factor – Wolfram MathWorld Liste des nombres inusuels jusqu'à 100 2, 3, 5, 6, 7, 10, 11, 13, 14, 15, 17, 19, 20, 21, 22, 23, 26, 28, 29, 31, 33, 34, 35, 37, 38, 39, 41, 42, 43, 44, 46, 47, 51, 52, 53, 55, 57, 58, 59, 61, 62, 65, 66, 67, 68, 69, 71, 73, 74, 76, 77, 78, 79, 82, 83, 85, 86, 87, 88, 89, 91, 92, 93, 94, 95, 97, 99.

Recherche particulière

On cherche les nombres tels que PGF(n² - 1) < 100.

La plus grande solution est: 19 182 937 474 703 818 751.

Cette information et d'autres en "on the largest prime factor of x² - 1 – Florian Luca et Filip Najman

Suite	Records Types de nombres selon leurs diviseurs Voir en haut de page Liste des nombres et leurs facteurs et diviseurs Multiensemble et factorisation des nombres
Voir	Calcul mental – Index Conjecture ABC Diviseurs – Développements théoriques Diviseurs – Somme en puissance Divisibilité Fonctions arithmétiques Géométrie – Index Machine des frères Carissan Nombres composés Nombres hautement composés Nombres parfaits PGCD Premiers Théorie des nombres – Index Types de nombres selon leurs diviseurs
Site	OEIS A006530 - Gpf(n): greatest prime dividing n Popular values of the largest prime divisor function – Nathan McNew – 2015 – Niveau avancé
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Decompos/FactPlGd.htm