|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
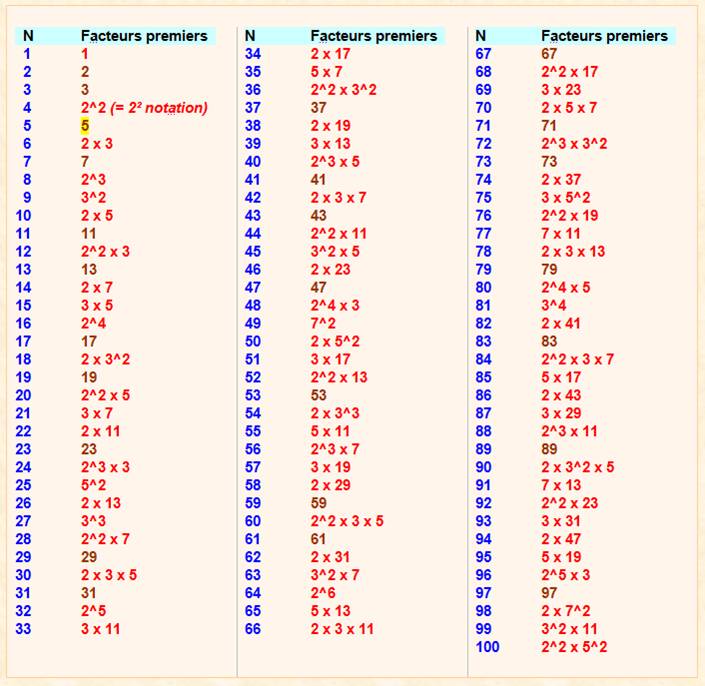
DIVISEURS PREMIERS FACTEURS PREMIERS (abrégé en FACTEURS) Sur
cette page: la table des facteurs des nombres jusqu'à 100; une propriété
singulière de la quantité de facteurs (conjecture de Polya); et la
programmation du calcul de la quantité de facteurs d'un nombre. En fin de
page, programmation Scratch de la factorisation des nombres. |
Théorème
|
Théorème
de Hardy-Ramanujan (1917):
Alors,
pour presque tous les entiers:
ω(n) = log log n |
|
|
|
|
Voir Suite
|
|
|
|
|||||||||||
|
Distance entre
premiers Records successifs de quantités de nombres
composés entre deux nombres premiers P1 & P2 Exemple entre 7 et 11
Tableau pour N <
1000 000
Record limite La valeur du record
limite est infinie: il est toujours possibles de trouver une suite de
nombres composés aussi grande que l'on veut
>>> |
|||||||||||
Nombres premiers et quantité de facteurs de
leurs successeurs
|
5 premier => 2 facteurs |
6 = 2x 3 => 2 facteurs |
|
|
29 premier => 2 facteurs |
30 = 2x3x5 => 3 facteurs |
|
|
13 premier => 2 facteurs |
14 = 2x7 => 2 facteurs |
15 = 2x5 => 2 facteurs |
|
103 premier => 2 facteurs |
104 = 23x13
=> 2 facteurs |
105 = 3x5x7 => 3 facteurs |
|
1153 premier => 2 facteurs |
1154 = 2x577 => 2 facteurs |
1155 = 3x5x7x11 => 4 facteurs |
|
3001 premier => 2 facteurs |
3002 = 2x19x79 => 3 facteurs |
3003 = 3x7x11x13 => 4 facteurs |
|
|
||
|
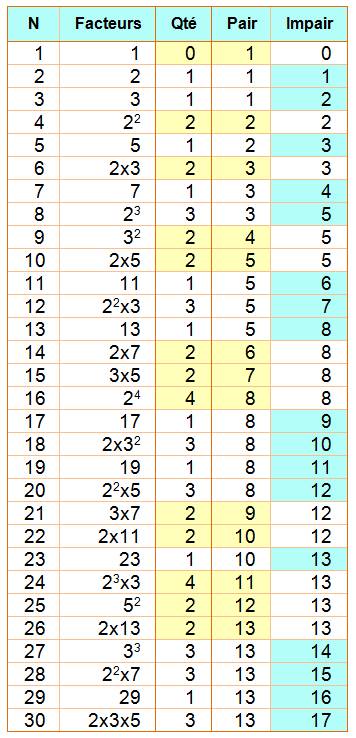
Le nombre 30 = 2 x 3 x 5 a
trois facteurs, soit une quantité impaire de
facteurs.
"Pairs" Les nombres qui ont une quantité impaire de facteurs sont plus
nombreux que ceux qui en ont une quantité paire. On conjecture que cela est
vrai pour tous les nombres jusqu'à l'infini. Eh bien non! Les "Pair"
dépassent les "Impairs" pour N = 906 150 257. J'ai arrêté les
calculs à N=90 608 968 avec les cumuls à 45 303 635 "Pairs" pour 45
305 332 "Impairs". |
|
|
|
EN 1919, Conjecture de Polya En 1958, réfutée par C.
Brian Haselgrove avec un nombre astronomique. En 1960, Sherman Lehman
trouve N = 906 180 359. En 1980, Minoru Tanaka donne
le plus petit contre-exemple
avec N = 906 150 257. |
||
Voir Fonction lambda de Liouville
qui caractérise la parité de la quantité de facteurs
Voir Nombres presque premiers et
développements sur la quantité des facteurs uniques ou répétés
|
|
||
|
Explications Le programme suivant calcule
la quantité de facteurs dans un nombre donné (N). Ici N= 120 = 23 x
31 x 51 écrit informatiquement [2, 3], [3, 1], [5, 1]. La quantité de facteurs distincts est 3. Tandis que la quantité de facteurs (totale) est: 3 + 1 + 1 = 5. C'est la
somme des exposants de chacun des facteurs distincts. En effet: 120 = 2 x 2 x
2 x 3 x 5. Programme expliqué pas
à pas
|
||
|
Programme calculant
les "Pair" et "Impairs"
|
QP est la quantité de nombres dont la
quantité de facteurs est paire; QI, même chose pour les impairs. Le cœur du programme est le même que
ci-dessus. Il est enveloppé par une boucle qui fait défiler les nombres N de
1 à 30 dans cet exemple. Notez l'emploi
du modulo 2 (reste de la division par 2)
pour reconnaitre si un nombre est pair ou impair Le début de la sortie:
Suite >>>
|
|
Voir Programmation de la
fonction lambda – Exemple de concision en programmation
Voir Programmation sur la recherche
de la quantité des facteurs uniques ou répétés
Curiosité – Relation entre facteur et
diviseurs
|
Quels
sont les nombres n tels que la quantité de diviseurs (tau) du produit des
facteurs (gamma) est égale au nombre lui-même |
|
|
Exemple Nombre
12 Ses
facteurs premiers: ( 2 , 3) Produit:
2 x 3 x 12 = 72 Quantité
de diviseurs de 72: 12 |
Les quatre seules solutions 1, {}, 1, 1 3, {3}, 9, 3 4, {2}, 8, 4 12,
{2, 3}, 72, 12 |
|
|
Programme Ouverture
des logiciels de théorie des nombres. Boucle
sur n et pour chacun: A est l'ensemble des facteurs. Produit
des facteurs et du nombre n et calcul du nombre de diviseurs (tau). Sortie
si on retrouve le nombre n. |
![]()
|
|
||
|
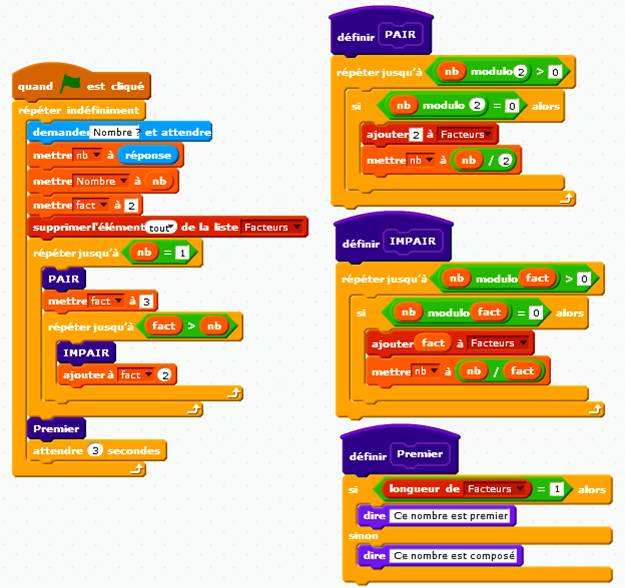
Le logiciel Scratch est accessible gratuitement
sur Internet (en ligne ou sur votre ordinateur) Avec ce programme vous disposer d'un outil à
votre main pour trouver les facteurs des nombres. Si vous cherchez les facteurs
de grands nombres, le calcul prendra du temps. Pour vérifier que le programme
est toujours en action, rendez visible la variable fact. |
||
|
Programme principal Il permet d'indiquer le nombre à factoriser: Nombre restera affiché, tandis que nb sera mis à jour au fur et à mesure de la
découverte des facteurs et cela jusqu'à ce que nb soit égal à 1. Pour commencer, le programme demande d'entrer un
nombre dans la fenêtre qui s'ouvre. Ce programme va d'abord chercher les facteurs
pairs dans nb, puis ses facteurs impairs.
Il fait appel à deux blocs, deux sous-programmes. Avant tout, fact
est mis à 2, puis à trois avant d'attaquer les impairs; et, on lui ajoute 2
pour traiter l'impair suivant. Ce programme traite un nombre, indique les
facteurs et spécifie si le nombre est premier
ou composé.
Après une attente de 3 secondes, il est prêt pour traiter un autre nombre. |
Sous-programme PAIR On cherche la quantité de facteurs 2. Répétitions tant que le nombre reste pair. Arrêt
dès que la division par 2 (modulo 2) donne
un reste supérieur à 0. Si, on peut diviser par 2, on le divise et on
ajoute un facteur 2 dans la liste des facteurs. Sous-programme IMPAIR On répète ce sous-programme pour trouver combien
de fois le facteur fact existe dans nb. Si, nb peut
diviser par fact, on le divise et on
ajoute ce facteur dans la liste des facteurs. Sous-programme Premier Selon la taille de la liste des facteurs, le
programme indique si le nombre est premier ou composé. |
|
|
|
||
Voir Programmation – Scratch
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
|
![]()