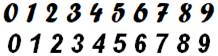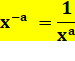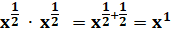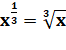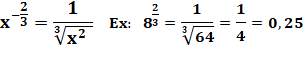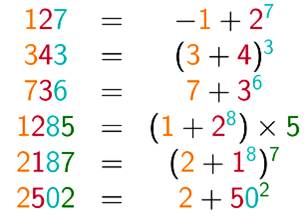NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 07/12/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Maths en se divertissant
Débutants Général	BRÈVES de MATHS									Glossaire Général
INDEX Brèves Atlas des maths	Page 1	Page 10		Page 20		Page 30		Page 40			Page 50
	Page 30 (480-599)		Page 31 (600-619)		Page 32 (620-639)		Page 33 (640-659)		Page 34 (660-679)
	Page 35 (680-699)		Page 36 (700-719)		Page 37 (720-739)		Page 38 (740-759)		Page 39 (760-779)

BRÈVES de MATHS – Page 30

Un millier de faits et chiffres

sur les nombres et les mathématiques

Ces pages sont dédiées à tous ceux qui veulent aborder les mathématiques en douceur et en s'amusant tout en découvrant les aspects les plus fondamentaux de cette discipline. Un parcours à picorer avec nombreux liens d'orientation vers les développements destinés à satisfaire votre curiosité.

En principe ces pages sont très abordables sans connaissances particulières de maths. Elles sont proposées dans un ordre quelconque favorisant la découverte de sujets multiples.

Anglais: Facts and figures about numbers and mathematics

580. Carré et dominos
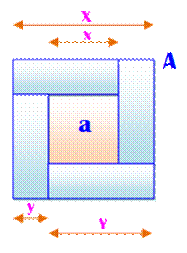
Énigme Un carré et quatre rectangles sont ainsi disposés pour former un grand carré. On sait que l'aire du grand carré (A) vaut quatre fois celle du carré interne (a) Quelle est le rapport entre la longueur (Y) de chaque rectangle et leur largueur (y) ? Solution en calculant les aires
Brèves associées	>>> Les neuf points en un seul trait	>>> Graphe pentagonal à colorier
Pour en savoir plus	>>> Carrés – Diverses curiosités	>>> Carré – Index

581. Carré rigide – Barres identiques
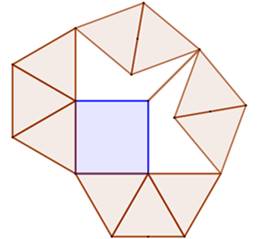
But Constituer un réseau de barres identiques sans croisement, comportant un carré et les éléments nécessaires pour le rigidifier. Solution La solution minimale consiste à composer cette figure comportant 4 + 23 = 27 barres Publiée par Martin Gardner (1964)
Brèves associées	>>> Polygones rigides		>>> Brèves constructions – Index
Pour en savoir plus	>>> Carré rigide avec barres identiques		>>> Polygones – Introduction et index

582. Théorème de Descartes-Euler
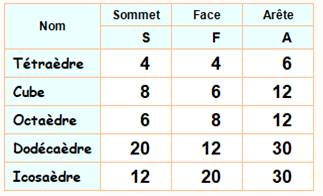
Invariant des polyèdres convexes
Brèves associées	>>> Polygones		>>> Brèves géométrie – Index
Pour en savoir plus	>>> Relation d'Euler pour les polyèdres		>>> Polyèdres

583. Florilège Repdigits et Pannumériques

Racine de repdigits

Propriété des premières décimales

n		n		n
11	3,3…	1111	33,33…	111111	333,333…
44	6,6…	4444	66,66…	444444	666,666…
99	9,9…	9999	99,99…	999999	999,999…

n
111111111111	333333,33333317…
444444444444	666666,66666634…
999999999999	999999,99999951…

Suite sans fin …

Division des retournés

n	nR	n / NR
21	12	1,7 50000000
321	123	2,6 09756098
4321	1234	3,5 01620746
54321	12345	4,4 00243013
654321	123456	5,3 00034020
7654321	1234567	6,2 00004536
87654321	12345678	7,1 00000583
987654321	123456789	8,0 00000073

Les deux premiers chiffres significatifs du quotient:

le premier vaut le premier chiffre de gauche moins 1, et

le second est son complément à 8.

Racine des nombres palindromes "en toit"

(En référence à la symétrie par rapport au chiffre central)

n
121	11
12321	111
1234321	1 111
123454321	11 111
12345654321	111 111
1234567654321	1 111 111
123456787654321	11 111 111
12345678987654321	111 111 111

Amusements sur calculette

proposés par Paul Villemin

Brèves associées

>>> Repdigits en 2 au cube

>>> Brèves motifs – Index

Pour en savoir plus

>>> Racine carré

>>> Racine carrée de repdigits

>>> Chiffres en puissance

>>> Nombres palindromes

>>> Nombres ondulants

>>> Docteur Villemin

584. Multiplication et distributivité
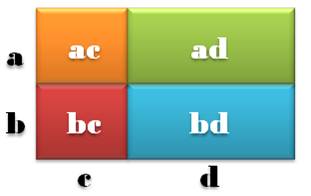
Comment comprendre et se souvenir des règles de distributivité en algèbre ?		Un simple dessin permet de reconstituer le développement du produit.
a (b + c) = ab + ac		(a + b) (c+ d) = ac+ ad + bc + bd
Brèves associées	>>> Identités remarquables		>>> Brèves Algèbre – Index
Pour en savoir plus	>>> Base de l'algèbre		>>> Piège, tracas en algèbre

585. Identité remarquable
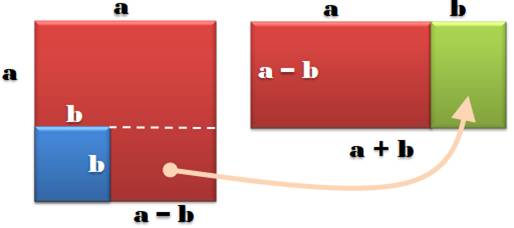
a² – b² = (a + b) (a – b) Exemple: 101² – 100² = (101 + 100) x 1 = 201 Démonstration muette
Brèves associées	>>> Identité de Brahmagupta	>>> Brèves Identités – Index
Pour en savoir plus	>>> Identités remarquables	>>> Piège, tracas en algèbre

586. Aire max selon périmètre
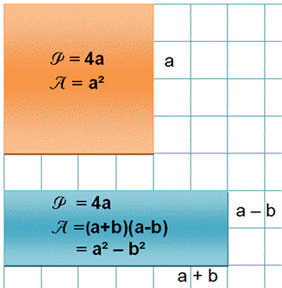
Quadrilatère Selon le dessin, le plus grand terrain rectangulaire entouré avec une corde de 40 m, sera un carré de 40 / 4 = 10 m et son aire sera 100 m². D'une manière générale, le côté du carré sera toujours le périmètre divisé par 4. Cercle On fera mieux avec un cercle. Aire en fonction du périmètre:
Brèves associées	>>> Carré divisé – Aire manquante		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Problème de Didon		>>> Carré

587. Tous les chiffres en 84
Avec ce simple 84 écrit de cette manière, il est possible de dessiner tous les chiffres de 0 à 9. Avec cette graphie, le 7 est rendu sans sa barre, comme sur les claviers ou comme l'écrivent les Américains. Même remarque pour le 4.
Brèves associées	>>> Compter avec dix chiffres		>>> Brèves Nombres – Index
Pour en savoir plus	>>> Nombre 84		>>> Écriture des chiffres >>> Sept barré ou non

588. Puissances négatives
On sait que x^4 = x.x.x.x Mais que vaut x^- 4, avec un exposant négatif? On utilise la propriété suivante:			On a, selon la propriété: Et également: En divisant par x^a
Brèves associées	>>> Puissance – Introduction	>>> Brèves Puissances – Index
Pour en savoir plus	>>> Puissances	>>> Puissances – Index

589. Puissance fractionnaire
Prenons un exemple et suivons la logique vue ci-dessus: On a aussi cette relation: En rapprochant ses deux égalités, on déduit:		Quelques exemples:
Brèves associées	>>> Puissance – Introduction		>>> Brèves Puissances – Index
Pour en savoir plus	>>> Puissances		>>> Puissances – Index

590. Simplification par télescopage

Méthode de simplification par annulation de termes de proche en proche.

Exemple avec la démonstration de la somme des entiers

Disons que S(n) = 1/2 n (n +1) et prouvons-le.

Dans le tableau, notons les différences de sommes pour n, n- 1, n-2, … 2, 1 et calculons. En notant que S(n) – S(n–1) = n.

n	S(n)	– S(n-1)	=	n
n – 1	S(n-1)	– S(n-2)	=	n – 1
n – 2	S(n-2)	– S(n-3)	=	n – 2
…
3	S(3)	– S(2)	=	3
2	S(2)	– S(1)	=	2
1	S(1)	– S(0) = 0	=	1
Somme	S (n)	– 0	=	S. Entiers

Les termes jaunes s'annulent et de même pour la suite.

Brèves associées

>>> Démonstration par récurrence

>>> Brèves Outils – Index

Pour en savoir plus

>>> Télescopage dans le DicoMot Math

>>> Somme des entiers

591. Carré = Somme de cubes
Démonstration muette Carré Aire du grand carré: (1+2+3+4+5)² = 15² = 225 Cubes Les carrés rouges de la diagonale ont une aire égale à : 1², 2², 3², 4², 5². Chacun de ces carrés de côté k est représenté par des carrés latéraux, vers la gauche et vers le haut, de même dimension, sauf pour k = 2 et k = 4 pour lesquels les rectangles s'assemblent pour former un carré de la dimension voulue. Ainsi, un carré k² est représenté k fois, soit k^3. L'aire du grand carré compté avec ces carrés élémentaires est donc formée d'une addition de nombres au cube. Théorème (1 + 2 + 3 +…+ n)^2 = 1^3 + 2^3 + 3^3 + … + n^3		Le plus grand carré de 5×5 est présent 5 fois, ce qui représente une aire égale 5^3. Même principe pour les carrés plus petits.
Brèves associées	>>> Carré = Somme de cubes >>> Cubes et caré de sommes		>>> Brèves Puissances – Index
Pour en savoir plus	>>> Carré, somme de cubes		>>> Carrés >>> Cubes

Merci à Daniel Fuks

592. Nombres orphelins
Le "fils" d'un nombre est défini de cette façon: chacun de ses chiffres est la différence absolue des deux chiffres successifs du "père". Ainsi le nombre 9370 a pour fils le nombre 647. Un père n'a qu'un fils, mais un fils peut: avoir plusieurs père (111 a 64 pères ou antécédents); n'avoir aucun père. Ce sont les nombres orphelins. Le plus petit est 648.		Si 648 est orphelin, alors son retourné 848 l'est aussi.
Brèves associées	>>> Nombres automorphes		>>> Brèves Motif – Index
Pour en savoir plus	>>> Nombres orphelins		>>> Nombres à motif – Index

593. Partition de 10
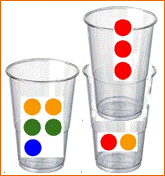
Énigme Trois verres et dix jetons (ou dix pièces). Placer un nombre impair de jetons dans chaque verre. Huit partitions à trois termes du nombre 10 [3, 3, 4], [2, 4, 4], [2, 3, 5], [1, 4, 5], [2, 2, 6], [1, 3, 6], [1, 2, 7], [1, 1, 8] Chacune comporte un ou trois nombres pairs.		Solution Le nombre 10 est pair et la somme de trois nombres impairs est impaire. Solution impossible sans une astuce ! Celle-ci consiste à mettre un gobelet dans un autre. Ils contiennent alors 5, 3, 5 jetons, des nombres impairs comme demandé.
Brèves associées	>>> Le faux billet de 50 euros		>>> Brèves Énigmes – Index
Pour en savoir plus	>>> Énigmes avec des verres		>>> Énigmes avec le nombre 10

594. Cercles dans le carré
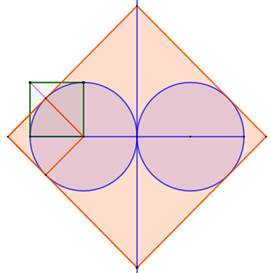
Construction Deux cercles tangents. Construire le carré circonscrit. Méthode Droite joignant les centres des deux cercles. Carré (vert) sur un rayon externe. Intersection cercle avec diagonale du carré. Carré (orange) porté par la diagonale. Perpendiculaire verticale au point de tangence des deux cercles (bleue). Droite portée par un côté du carré orange. Intersection avec la perpendiculaire bleue. Grand carré orange sorte d'extension du petit carré orange. Sauriez-vous calculer le rayon de ces cercles en fonction du côté du carré ? >>>
Brèves associées	>>> Cercle de Ford		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Les deux cercles dans le carré		>>> Cercle – Index

595. Volume de la boite
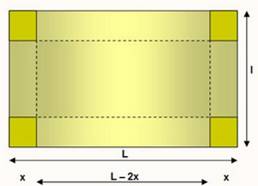
Problème On confectionne une boite à partir de ce patron. Quelles sont ses dimensions pour obtenir le volume maximum. Pas si simple ! Calcul du volume Longueur = L – 2x Largeur = l – 2x Volume = (L – 2x) ( l – 2x ) x = x ( L . l – 2xL – 2xl + 4x²) V = 4x^3 – 2x² (L + l) + x . L . l Volume maximum Application du calcul des dérivées: la fonction volume V(x) atteint un extremum lorsque sa dérivée par rapport à x est nulle. Dérivée de V(x): V'(x) = 12x² – 4 (L + l) + L . l Exemple L = 200 mm et l = 100 mm V'(x) = 12x² – 1200x + 20 000 Solution positive pour x = 21,13 Alors L = 157,73 mm, l = 57,73 mm et V = 192 450 mm^3
Brèves associées	>>> Calcul différentiel et intégral	>>> Brèves Analyse – Index
Pour en savoir plus	>>> Calcul du volume max de la boite	>>> Dérivées

596. Carré magique et carrés
Le carré magique 3x3 est unique. Parmi ses propriétés, celle-ci: On forme des nombres en lisant les chiffres des lignes ou des colonnes (comme 618). On prend son retourné (816). Alors, la somme des carrés (en rouge) pour les trois lignes est égale à la somme des carrés des retournés pour ces trois lignes. Même chose avec les colonnes.
Brèves associées	>>> Carré magique 3x3 – Permutations	>>> Brèves Énigmes – Index
Pour en savoir plus	>>> Somme des carrés dans le 3x3	>>> Carrés magiques – Index

597. Suite de nombres composés
On s'intéresse aux nombres premiers successifs. On sait que l'écart minimal est 2 pour les nombres premiers jumeaux (comme les nombres premiers 11 et 13, séparés par un seul nombre composé). Mais, existe-il une limite pour la plus longue suite ? Par exemple, il y a sept nombres composés entre 89 et 97 (illustration), soit un intervalle de 8 entre les deux premiers. 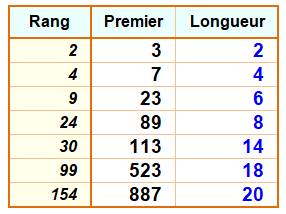En fait, on sait trouver des suites aussi longues que l'on veut, voire infinie ! Mais, quelles sont celles connues ? Le tableau montre le début de la liste de longueur record pour le plus petit nombre premier en tête de la liste. En 2020, le record de longueur est 1510. Les ordinateurs continuent de tourner …
Brèves associées	>>> Dizaines sans nombre premier		>>> Brèves Premiers – Index
Pour en savoir plus	>>> Écarts entre nombres premiers >>> Nombres premiers jumeaux		>>> Nombres premiers

598. Nombres de Friedman
Nombres qui peuvent être exprimés en utilisant les chiffres associés à des opérateurs arithmétiques classiques. Comme 25 = 5² ou 1024 = 4^10 / 2. Ils sont très nombreux. Ils sont Friedman bien ordonnés si les chiffres sont placés dans l'ordre comme pour les exemples à droite. Ils sont Friedman sauvages s'ils utilisent des opérateurs autres que les quatre opérations. Comme:		Exemples de Nombres de Friedman bien ordonnés
Brèves associées	>>> Nombres de Harshad		>>> Brèves Nombres – Index
Pour en savoir plus	>>> Nombres de Friedman >>> Nombres de Friedman sauvages		>>> Nombres cousins de Friedman >>> Nombre 24

599. Chiffres concaténés
Nombres chiffres concaténés Les 45 nombres formés avec tous les chiffres dans l'ordre croissant et possibilité de concaténation. Ainsi, 123 est valide car il est le regroupement en un nombre (concaténation) de trois chiffres consécutifs.		1, 2, 3, 4, 5, 6, 7, 8, 9, 12, 23, 34, 45, 56, 67, 78, 89, 123, 234, 345, 456, 567, 678, 789, 1234, 2345, 3456, 4567, 5678, 6789, 12345, 23456, 34567, 45678, 56789, 123456, 234567, 345678, 456789, 1234567, 2345678, 3456789, 12345678, 23456789, 123456789.
Nombres somme de chiffres concaténés Il y a 187 nombres formés par la somme des nombres chiffres concaténés de sorte que tous les chiffres de 1 à 9 soient représentés en ordre croissant. Ainsi: 126 = 12 + 3 + 4 + 5 + 6 + 7 + 89		45, 54, 63, 72, 81, 90, 99, 108, 117, 126, …, 456813, 456912, 1234584, 1234656, 2345688, 3456792, 3456801, 12345687, 23456790.
Multiples de 9 Toutes ces sommes sont des multiples de 9 car la somme des chiffres est un multiple de 9. Certains multiples de 9 sont intouchables par ces sommes. Le plus petit étant 243.		243, 297, 306, 351, 360, 369, 405, 414, 423, 468, 477, 522, 531, 540, 585, 639, 648, 657, 765, 774, 792, 801, 900, 909, 918, 936, 945, 954, 981, 990, 999, 1008, …
Brèves associées	>>> Nombres automorphes		>>> Brèves Nombres – Index
Pour en savoir plus	>>> Somme des chiffres concaténés		>>> Nombres et chiffres – Index >>> Divisibilité par 9

Retour	Brèves de maths – Page 29
Suite	Brèves de maths – Page 31
Voir	Voir liens en haut de page
Sites	Somme ces n premiers cubes – Wikipédia
Cette page	http://villemin.gerard.free.fr/NombDico/aBreves/Breve30.htm