|
||||||||||||||||||||||||||||||||||||||||
![]()
|
FORMULE d'EULER n² + n + 41 = n (n+1) + 41 Parcours
autour de cette formule trouvée en 1772 par Euler (1707-1783) qui produit de nombreux
nombres premiers, notamment pour tous les nombres n de 0 à 39. Avec ce polynôme, pratiquement six nombres sur
10 sont premiers (58) jusqu'à n = 1 000. Si ce polynôme quadratique n'est pas
le plus productif, il a un double intérêt: historique et simplicité (produit
de deux nombres consécutifs plus 41). Le
polynôme n² – n + 41 = n (n – 1) + 41, trouvé
par Legendre est équivalent à celui d'Euler. Le polynôme n² – 79n + 1600 est lui aussi un cousin de celui d'Euler
par changement de variables (n devient n – 40). Les
nombres premiers en n² + n + k sont les chanceux d'Euler, baptisés ainsi par F. Le Lionnais
(1983). Le critère de Rabinowitch permet de dire que 41 est la plus grande
valeur produisant le plus de premiers. |
Voir Spirale d'Ulam / Barre magique des nombres premiers
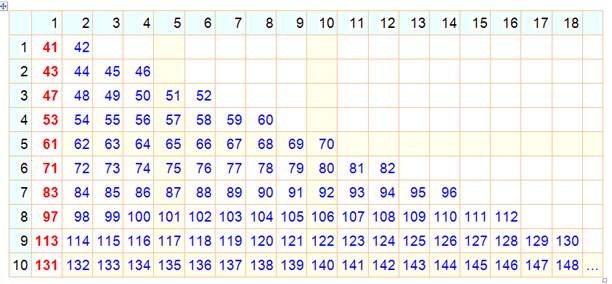
Nombres premiers en n² + n + 41 pour n de 0 à 100
|
Nombres premiers [41,
43, 47, 53, 61, 71, 83, 97, 113, 131, 151, 173, 197, 223, 251, 281, 313, 347,
383, 421, 461, 503, 547, 593, 641, 691, 743, 797, 853, 911, 971, 1033, 1097,
1163, 1231, 1301, 1373, 1447, 1523, 1601, 1847, 1933, 2111, 2203, 2297, 2393,
2591, 2693, 2797, 2903, 3011, 3121, 3347, 3463, 3581, 3701, 3823, 3947, 4073,
4201, 4463, 4597, 4733, 4871, 5011, 5153, 5297, 5443, 5591, 5741, 6047, 6203,
6361, 6521, 7013, 7351, 7523, 7873, 8231, 8597, 8783, 8971, 9161, 9547, 9743,
9941, 10141] Tous les nombres avec 1 s'il est premier et 0 s'il est composé [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 1,
1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1,
1, 0, 1, 1, 1, 1] Il
y 14 composés sur ces 101 nombres. |
|
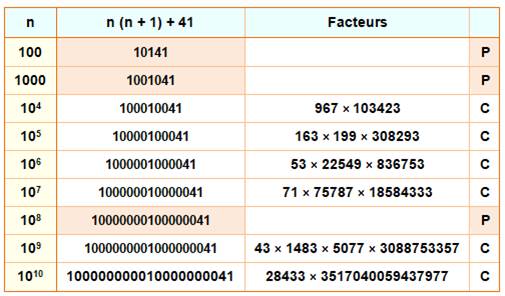
La
formule étant n
(n + 1) + 41, si
n est une puissance de 10, on obtient un nombre caractéristique: il commence
par n + 1 et se termine par 41.
Notez que l'on obtient le nombre lui-même en
tête en utilisant la formule en n (n – 1) + 41. Notez qu'il existe une grande quantité de
nombres p se terminant par 41. La liste commence pour n = {0, 24, 75, 99,
100, 124, 175, 199, 200, 224 …} |
Merci à Ivan Gauvin pour ses remarques
![]()
|
|
|
|
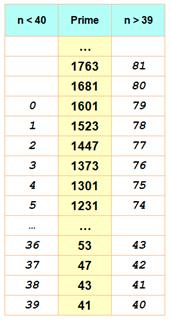
Remarquez la similitude des unités! Avec 17, 19, 23 … 257, on trouve 16 nombres premiers Remarquez que chacune de ces trois séquences comporte n
– 1 nombres premiers, n étant le nombre de tête. Autre curiosité avec 41:
|
|
Voir Premiers en
constellations
Historique
|
En
1772, Euler écrit à Daniel Bernoulli, en réponse à un mémoire écrit en 1771: Cette progression 41, 43, 47, 53, 61, 71,
83, 97, 113, 131, etc. dont le terme général est 41x + x², est d'autant plus
remarquable que les 40 premiers termes sont tous des nombres premiers. |
|
FORMULE en 41 |
|
|
|
P = n² + n + 41 Alors P est premier
pour n de 0 à 39. P est un polynôme quadratique. Note
P = n² – n + 41 = (n – 1) n
+ 41 (Legendre)
|
0 41 1 43 2 47 3 53 4 61 5 71 6 83 7 97 8 113 |
|
|
|
||||||||||||||||
|
Voir Comparaison
avec les autres formules Il n'existe pas de formule: x² + ax + b, avec des coefficients positifs et
inférieurs à 10 000, qui produise une plus longue suite de nombres
premiers. >>> Équation: x² + x + 41
= 0 son discriminant est b² - 4ac = -163
Graphe de la fonction:
x² + x + 41
|
||||||||||||||||
Voir Spirale
d'Ulam avec 41 au centre
|
ou
composés |
|
|
p = n² + n + C Voir Représentation graphique de ces
nombres avec la spirale d'Ulam
n² + n = n (n + 1) n²
- n = (n - 1) n
Liste
pour n de 1 à C – 2: Avec ces valeurs
de C, tous les nombres obtenus sont premiers. C = 3, [5] C = 5, [7, 11, 17] C = 11, [13, 17,
23, 31, 41, 53, 67, 83, 101] C = 17, [19, 23, 29,
37, 47, 59, 73, 89, 107, 127, 149, 173, 199, 227, 257] C = 41, [43, 47, 53, 61, 71, 83, 97, 113, 131, 151, 173, 197, 223, 251, 281, 313, 347, 383, 421, 461, 503, 547, 593, 641, 691, 743, 797, 853, 911, 971, 1033, 1097, 1163, 1231, 1301, 1373, 1447, 1523, 1601] Tableau des nombres produits par la formule selon la valeur de
C et indication des nombres premiers
Liste
des quantités de nombres premiers pour c de 1 à 200 par tranches de 25 32, 0, 14, 0, 29, 0,
31, 0, 13, 0, 48, 0, 18, 0, 11, 0, 59, 0, 25, 0, 14, 0, 28, 0, 28, 0, 16, 0, 34,
0, 35, 0, 11, 0, 24, 0, 36, 0, 17, 0, 86, 0,
15, 0, 12, 0, 47, 0, 21, 0, 17, 0, 28, 0, 19, 0,
12, 0, 50, 0, 28, 0, 7, 0, 25, 0, 50, 0, 19, 0, 36, 0, 24, 0, 10, 0, 39, 0, 25, 0, 22,
0, 38, 0, 19, 0, 15, 0, 30, 0, 29, 0, 12, 0, 42, 0, 30, 0, 11, 0, 67,
0, 15, 0, 10, 0, 68, 0, 28, 0, 19, 0, 20, 0, 19, 0, 14, 0, 34, 0, 33, 0, 11,
0, 44, 0, 29, 0, 18, 0, 26,
0, 18, 0, 11, 0, 54, 0, 33, 0, 12, 0, 32, 0, 15, 0, 15, 0, 38, 0, 35, 0, 8, 0, 29, 0,
36, 0, 10, 0, 57, 0, 16, 0, 8, 0, 45, 0, 26, 0, 25, 0, 32, 0, 13, 0, 20, 0, 42, 0, 38,
0, 9, 0, 36, 0, 26, 0, 11, 0, 48, 0, 26, 0, 12, 0, 36, 0, 40, 0 Exemples
86 premiers pour n² + n+ 41 et 67 premiers pour n² + n + 101. |
|
Voir Tables
des premiers selon formules / Nombre 163
(Heegner)
|
Taux de productivité de nombres
premiers en fonction de C |
|
|
Exemple pour C = 41: 92% des nombres sont premiers jusqu'à n =
50; 59% le sont pour n jusqu'à 1000; et 41% pour n jusqu'à 10 000. |
|
|
|
|
|
|||
|
Sur la plage n de 0
à 1 000. |
|||
|
MAXIMUM
jusqu'à C
= 1 000 C Taux
en % 41 58,14 101 45,25 107 45,35 221 44,56 227 44,36 347 41,16 377 41,76 389 41,46 551 40,06 587 42,56 671 45,25 857 42,66 881 43,56 941 46,55 |
MINIMUM
jusqu'à C
= 10 000 C Taux
en % 1155 3,79 2793 3,99 3855 3,99 5643 3,59 6693 3,69 7005 3,69 7215 3,89 9135 3,59 9315 3,69 9525 3,49 9735 3,79 9933 3,39 |
MINIMUM
RECORD Valeurs
de C pour records successifs C
Taux en % 1 18,88 3 9,391 9 7,692 15 6,793 33 5,994 75 5,594 183 5,295 435 5,095 453 4,595 555 4,496 1 155 3,796 5 643 3,596 9 525 3,497 9 933 3,397 10 515 3,197 18 963 3,097 25 005 2,897 55 335 2,797 57 183 2,498 79 275 2,398 323 475 2,198 361 305 2,098 811 965 1,998 |
|
Conjecture F de Hardy et Littlewood
(1923) ***
|
La
recherche ci-dessus est intéressante et peut se poursuivre avec les moyens de
calcul d'aujourd'hui. Pourtant, "à la main", au début du siècle
dernier, Hardy et Littlewood formulent
une conjecture qui se rapporte à ce sujet. Elle explique certaines propriétés
de la spirale d'Ulam. La
conjecture s'applique aux polynômes quadratiques ax² + bx + c ou a, b et c sont
des entiers et a est positif. Si
a, b et c ont un facteur commun (> 1)
ou si b² - 4ac (discriminant)
est un carré parfait, alors ce
polynôme se factorise et produit donc des nombres composés pour presque
toutes les valeurs entières de x; de plus si a + b et c sont des nombres pairs, le polynôme donne des nombres
pairs. Sinon, le polynôme engendre une infinité de nombres premiers pour x
entier. La quantité de premiers P(n) est donnée par une formule un peu
compliquée que voici:
Explications en anglais: Paradox
– Melbourne University |
|
|
|
|
Par un changement de variable, il est
possible de former des polynômes cousins qui engendrent autant de nombres
premiers. Ici, n = N – k = N – 40.
Graphe et valeurs de
cette fonction
L'allure du graphe montre, ce qui est vrai,
que les premiers pour n de 0 à 79, sont dupliqués. Par exemple le premier 41
est produit pour n = 39 et n = 40. Généralisation La production de premiers est conservée
quelle que soit la valeur k. Avec k = 30, le minimum de la courbe est obtenu
pour n = 30 et la duplication est réduite d'autant. Théorème Si P(n) engendre des
premiers pour alors c'est le cas
pour P(N – k) avec Avec n = 2N + 42,
le polynôme d'Euler devient:
Graphe et valeurs de
cette fonction
Cette fois nous obtenons les premiers de
chaque côté de la courbe, pas en double. Encore des cousins …
Polynômes équivalent à celui d'Euler
Les fonctions sur la même lignes sont
équivalentes; elles produisent des premiers dans l'ordre inverse l'une de
l'autre. |
|
|
BILAN |
|
|
La densité de nombres premiers la plus
faible (1,99%) a été obtenue pour: C = 811 965 = 3 x 5 x 7 x 11 x 19 x 37 pour C exploré jusqu'à 1 000 000
C = 219 525 = 3 x 5² x 2927 avec 236 nombres premiers soit une productivité
de 2,36% C = 249 705 = 3² x 5 x 31 x 179 Fait mieux avec 234 nombres premiers soit
2,34% D'après Clifford Pickover (Magiques mathématiques) |
|
![]()
|
Voir |
|
|
|
|
|
DicoNombre |
|
|
|
|
|
Cette page |
![]()