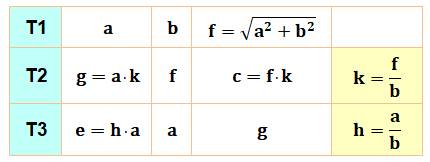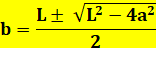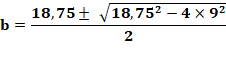Partage du rectangle en trois triangles semblables

Édition du: 10/07/2023

INDEX Géométrie	RECTANGLE
	Rectangle	Triangles dans rectangle	Cercles dans le rectangle
	Partage en 3 triangles	Carrés dans rectangle	Rectangle dans rectangle
		Rectangles – Énigmes

Faites un double-clic pour un retour en haut de page

Partage du rectangle

en trois triangles

Questions

Comment partager un rectangle en trois triangles de mêmes aires ou en trois triangles semblables? Quelles sont les conditions ? Comment construire la figure?

En bref

La dissection du rectangle est impossible pour trois triangles de même aire.

Pour les triangles semblables, la dissection n'est possible que pour: Longueur ≥ 2 fois la largeur.
Elle est donc impossible pour le carré.

Sommaire de cette page

>>> Partage en trois triangles de même aire ?

>>> Rectangle en trois triangles semblables

>>> Exemples de calcul

>>> Longueur du rectangle

Débutants

Géométrie

Glossaire

Géométrie

Partage en trois triangles de même aire ?

haut

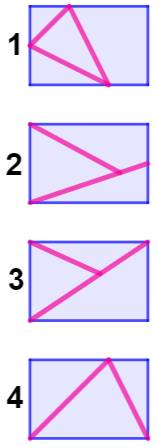
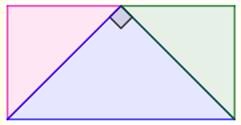
Problème

Un rectangle.

Comment le partager en trois triangles de même aire ?

Solution

C'est impossible.

Voyons quatre dispositions possibles.

1) Sommets du triangle sur les côtés du rectangle.
Un quadrilatère en trop.

2) Deux sommets du triangle sur les sommets du rectangle.
L'une des trois formes n'est pas un triangle.

3) Trois sommets du triangle sur les sommets du rectangle.
L'un des triangles occupe la moitié de la surface et non le tiers.

3) Deux sommets du triangle sur les sommets du rectangle et le troisième sur le côté opposé du rectangle.
Les trois triangles ont la même hauteur. Pour avoir la même aire, il faudrait qu'ils aient la même longueur de base. Ce qui est impossible.

Rectangle en trois triangles semblables

haut

Problème

Un rectangle. Comment le partager en trois triangles semblables ?

Requis

Pour former trois triangles deux des sommets doivent être situés sur les sommets du rectangle.

Si les trois triangles sont semblables, leurs angles sont égaux deux à deux.

Deux des triangles assemblés doivent créer des côtés parallèles pour épouser le rectangle. Ce sont donc des triangles rectangles.

Reste à faire en sorte que les angles soient égaux deux à deux.

Deux sommets sur sommets nécessaires

Triangles rectangles imposés

Exemples de calcul

haut

Problème

Un rectangle de dimension a = 9 et b = 12.

Calculer les longueurs des côtés des trois triangles.

Principe de calculs

La longueur de l'hypoténuse du premier triangle est calculée avec le théorème de Pythagore:
f² = a² + b²

Quant aux autres longueurs: on sait que dans les triangles semblables les proportions sont respectées.
On a les rapports d'homothétie suivants:
k = f / b et h = d / b

Calculs

T1	a = 9	b = 12	f = 15
T2	g = 11,25	f = 15	c = 18,75	k = 15 / 12 = 1,25
T3	e = 6,75	d = 9	g = 11,25	k = 9 / 12 = 0,75

L = c = 12 + 6,75 = 18,75

Longueur du rectangle				haut
Calcul littéral Le même calcul que ci-dessus. Longueur du rectangle L		Longueur de chacun des côtés
Un rectangle donné On connait a et L. Comment calculer b ? En littéral et en numérique. Les deux points trouvés sont symétriques par rapport au milieu du grand côté du rectangle.	Voir Équation 2^e degré		On retrouve bien la valeur de b = 12.
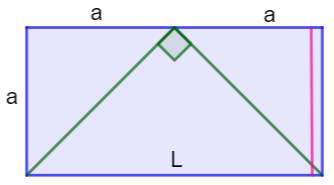
Cas limite Le partage est impossible pour L < 2a (trait rose). Cas limité pour L = 2a. Dans ce cas l'équation en b devient: (a – b)² = 0 et la racine est a = b. Si L < 2a, les racines de l'équation en b sont des nombres complexes.		Le rectangle ne peut être disséqué en trois triangles semblables que si la longueur vaut au moins deux fois la largeur. Donc pas de solution pour le carré.

Haut de page (ou double-clic)

Retour	Rectangle – Index
Suite	Cercles dans le rectangle Chèvre dans un champ rectangulaire Constructions élémentaires: rectangle Pavé droit Quadrilatères – Juniors Rectangle - Coordonnées intersection Rectangle dans quadrilatère cyclique Rectangles emboîtés Rectangles magiques Triangle dans rectangle – Aires
Voir	Allumettes Carré Construction à la règle et au compas Dénombrer – Index DicoMot Maths Énigmes classiques Géométrie – Index Jeux – Index
Cette page	http://villemin.gerard.free.fr/GeomLAV/Carre/RectTrg.htm