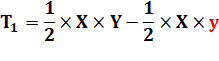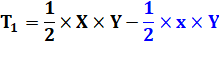|
Édition du: 18/11/2023 |
|
INDEX |
QUADRILATÈRES – Compter |
||
|
|
|||
![]()
|
TRIANGLES dans RECTANGLE Partage d'un
rectangle en triangles par une sécante. Propriétés. Comparaison des aires |
||
|
|
Sommaire de cette page >>>
Problème >>>
Approche >>>
Démonstration >>> Bonus – Propriétés du rectangle avec ses diagonales |
Débutants Glossaire |
|
|
||
|
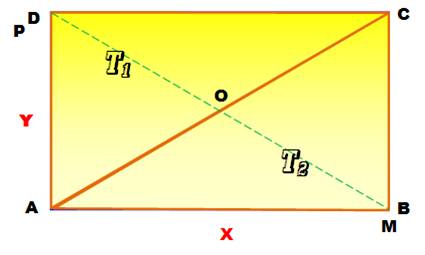
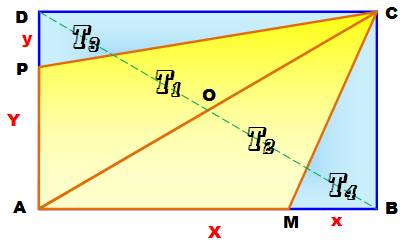
Un rectangle ABCD. Une parallèle quelconque à la
diagonale BD qui coupe le rectangle en P et M. Comparer
les triangles CPA
et CMA. |
Comparer les deux triangles
jaunes |
|
|
|
||
|
Recherche de pistes Visiblement
les deux triangles sont quelconques:
ni rectangles, ni isocèles. Les côtés
n'ont pas mêmes mesures; les triangles ne sont pas égaux. Les
angles sont différents; les triangles ne sont pas semblables. |
La
seule piste qui vient à l'esprit: la comparaison des aires. |
|
|
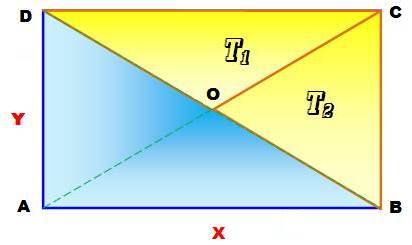
Recherche de cas particuliers Ayant le choix
du positionnement de la parallèle, pourquoi ne pas la choisir confondue avec
la diagonale? Alors P est en D et M est en B. Nous
avons deux triangles rectangles dont nous voulons comparer les aires:
Les aires
des triangles T1 et T2 sont égales et ce sera la même
chose avec une parallèle quelconque. (Normal! Ce sont chacun un demi-rectangle). |
En termes d'aires:
|
|
|
Une puce à l'oreille *… Qui dit
parallèle, dit théorème de Thalès
et, donc, des proportions qui sont conservées. Il est
sans doute intéressant de comparer les longueurs x et y. Visiblement, pas
égales! Le
triangle marron et le triangle rose sont rectangles, mais ce n'est pas le
plus important. Ils ont:
=> ils sont semblables. Le
théorème de Thalès s'applique => |
|
|
*
Les Anglais disent: it rings a bell: ça
sonne une cloche; ça me dit quelque chose.
Certains
invoqueraient l'intuition mathématique.
Pour
moi, il s'agit plutôt d'un réflexe intellectuel étant donné le champ des choses
apprises.
|
|
||
|
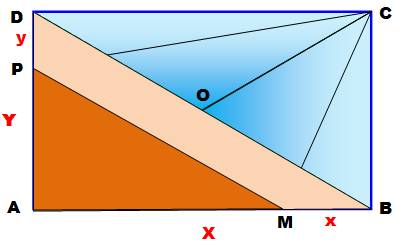
Aire de T1
= Aire du demi-rectangle – T3 Aire de T2
= Aire du demi-rectangle – T4
Or nous
connaissons y en fonction de x:
|
Les triangles T1 et T2 ont la même aire. De même, les triangles T3 et T4 ont même aire. Et cela quelle que soit la position de la parallèlePM à DB |
|
|
|
||
|
Prenons les triangles en jaune sur la figure:
Les aires des triangles T1 et T2 sont égales. Théorème Les quatre triangles découpés par les
diagonales ont la même aire, égale à un quart de celle du rectangle. |
En termes d'aires:
Et même chose pour leurs symétriques |
|
Anglais: Area of
diagonal-generated triangles in rectangles
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()