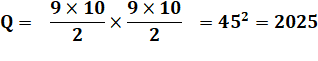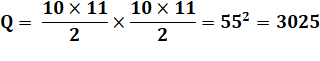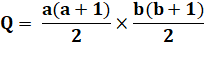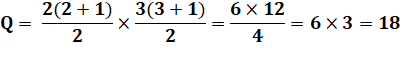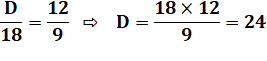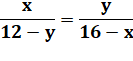|
Édition du: 20/02/2025 |
|
INDEX |
QUADRILATÈRES – Compter |
||
|
|
|||
Faites
un double-clic pour un retour en haut de
page
![]()
|
RECTANGLES dans un RECTANGLE Amusements avec des rectangles dans un rectangle. Rectangle inscrit dans un triangle: connaissant certaines dimensions,
calculez les autres. Attention, pas si simple! équation du quatrième degré à résoudre. |
||
|
|
Sommaire de cette page >>> Rectangles
dans grille 9 × 9 >>> Approche numérique >>> Bilan |
Débutants Glossaire |
|
Rectangles dans grille 9 × 9 |
|||
|
Problème Quelle
est la quantité de rectangles dans une grille de 9 par 9 rectangles (10
traits verticaux et 10 traits horizontaux). Naïvement Il
y a 9 × 9 = 81
rectangles. Ce sont les rectangles élémentaires. C'est
sans compter tous les rectangles formés de plusieurs rectangles élémentaires. Dénombrement Décompte
sur une bande horizontale, des rectangles les plus petits au plus grands: Décompte
selon la largeur de bande en vertical: = 45 × 45 = 2025 |
|
||
|
Formule pour 9 ×
9 et pour 10 × 10
|
Formule pour a ×
b
Voir Somme des entiers |
||
|
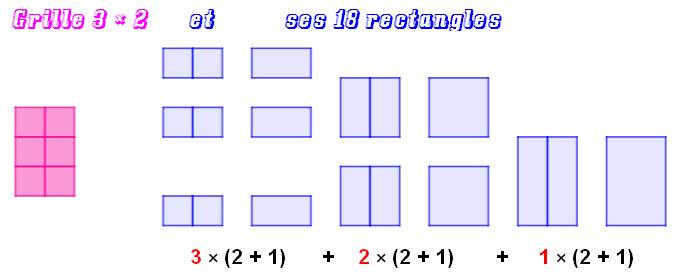
Exemple de grille "asymétrique": a = 2 et b = 3
Sur la figure: Q = 9 + 6 + 3 = 18 Avec la formule:
|
|||
|
Liste des quantités de rectangle (en rouge) par ordre croissant, avec la valeur de a et
b jusqu'a 10 |
[1, 1, 1], [3,
1, 2], [6, 1, 3], [9, 2, 2], [10,
1, 4], [15, 1, 5], [18, 2,
3], [21,
1, 6], [28, 1, 7], [30, 2, 4], [36,
1, 8], [36, 3, 3], [45, 1, 9], [45,
2, 5], [55, 1, 10],
[60, 3, 4], [63,
2, 6], [84, 2, 7], [90, 3, 5], [100,
4, 4], [108, 2, 8], [126, 3, 6], [135,
2, 9], [150, 4, 5], [165, 2, 10], [168,
3, 7], [210, 4, 6], [216, 3, 8], [225,
5, 5], [270, 3, 9], [280, 4, 7], [315,
5, 6], [330, 3, 10],
[360, 4, 8], [420,
5, 7], [441, 6, 6], [450, 4, 9], [540,
5, 8], [550, 4, 10],
[588, 6, 7], [675,
5, 9], [756, 6, 8], [784, 7, 7], [825,
5, 10], [945, 6, 9], [1008, 7, 8], [1155,
6, 10], [1260, 7, 9], [1296, 8, 8], [1540,
7, 10], [1620, 8, 9], [1980, 8, 10], [2025, 9, 9],
[2475, 9, 10], [3025,
10, 10] |
Voir Nombre 2025
![]()
|
Partage en quatre |
|
|
|
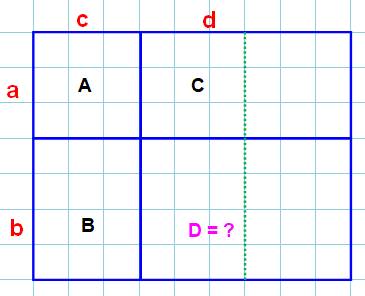
Problème Un rectangle est divisé en quatre par deux
droites parallèles aux côtés. On connait l'aire de trois rectangles (A, B et
C). Trouver l'aire du quatrième. Observation numérique Sur la figure A = 9, B = 12 et C = 18. On peut se dire que les aires sont
proportionnelles. Essayons: C'est bon ! Observation géométrique La ligne verte montre que les rectangles de
droite sont le double e ceux de droite (en surface). Si B = 12, alors D = 24. |
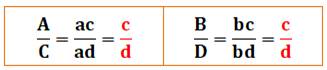
Calculs des proportions
|
|
Anglais: a rectangle is divided into four rectangles. What is the area of the
fourth rectangle ?
|
|
||
|
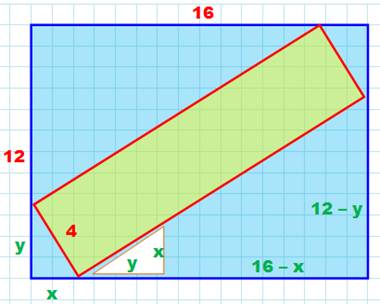
Problème Un
rectangle 16 x 12. Un
rectangle inscrit dont la largeur vaut 4. Trouvez
la valeur de x et la longueur L de ce rectangle. Mesures (pour ordre de grandeur et
vérification des calculs) x = 2,2 y
= 3,5 et L = 16,3 Remarque: similitude Le
triangle rectangle (x, y, 4) à été reporté dans le grand triangle rectangle
(figuré en blanc) pour mieux apprécier les rapports de similitude. |
|
|
|
La similitude des triangles permet
d'écrire: |
16x
– x² = 12y – y² |
|
|
Avec le théorème de Pythagore: |
y² = 4² – x² |
|
|
En remplaçant: |
16x
– x² = 12y – 16 + x² |
|
|
En isolant y: |
– 2x²+ 16x + 16 = 12y |
|
|
En élevant au carré et avec la valeur de y² |
(– 2x²+ 16x + 16)² = 12²
(4² - x²) |
|
|
Soit l'équation du quatrième degré: |
4x4
– 64x3 + 336x2 + 512x – 2048 = 0 |
|
|
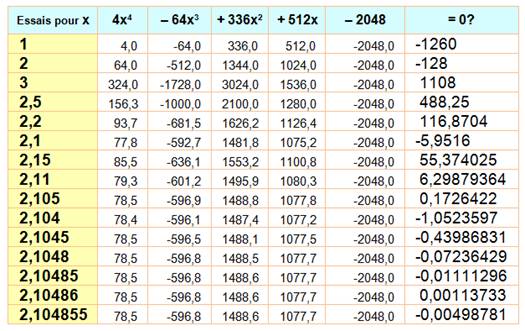
Avec calculette,
logiciel mathématique ou tableur Quatre solutions dont une négative et deux
complexes à rejeter. |
x
= 2,104 859 071 586 42 … |
|
|
Valeur de y |
y²
= 16 – x² => y = 3,401406810… |
|
|
Longueur du rectangle central |
L²
= (16 – x)² + (12 – y)² L = 16,34046347… |
|
|
Possibilité de trouver la solution à l'équation
avec tableur. On procède par approche progressive (plus ou
moins: dichotomie) |
|
|
Inutile
de donner la formule littérale. Il s'agit d'une équation du quatrième degré.
Autant la calculer directement avec les valeurs numériques. Il
existe d'autres problèmes intéressants du même type:
|
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()