NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 01/11/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Maths en se divertissant
Débutants Général	BRÈVES de MATHS									Glossaire Général
INDEX Brèves Atlas des maths	Page 1	Page 10		Page 20		Page 30		Page 40			Page 50
	Page 30 (480-599)		Page 31 (600-619)		Page 32 (620-639)		Page 33 (640-659)		Page 34 (660-679)
	Page 35 (680-699)		Page 36 (700-719)		Page 37 (720-739)		Page 38 (740-759)		Page 39 (760-779)

BRÈVES de MATHS – Page 38

Un millier de faits et chiffres

sur les nombres et les mathématiques

Ces pages sont dédiées à tous ceux qui veulent aborder les mathématiques en douceur et en s'amusant tout en découvrant les aspects les plus fondamentaux de cette discipline. Un parcours à picorer avec nombreux liens d'orientation vers les développements destinés à satisfaire votre curiosité.

En principe ces pages sont très abordables sans connaissances particulières de maths. Elles sont proposées dans un ordre quelconque favorisant la découverte de sujets multiples.

Anglais: Facts and figures about numbers and mathematics

Spécial QUIZZ Géométrie

On trouve parfois ces énigmes sur les réseaux sociaux avec ou sans solution …

Une sélection de 20 problèmes par ordre croissant de difficulté.

740. Dans le carré
Énigme Un carré dont le côté est donné. F milieu de CD et G milieu de AF. Longueur x de BG ? Solution La figure de droite indique les valeurs faciles à calculer. Notamment la position du point G en (a, 2a) Avec le théorème de Pythagore: x² = (2a)² + (3a)² = 13a²	Méthode pour la construction de la racine de 13

Voir Carré manquant et autres énigmes relatives au carré

741. Carrés dans un cercle
Énigme Un cercle et deux carrés. Le carré rose a un côté posé sur un diamètre et les deux autres sommets sur la circonférence. Le second carré a deux sommets opposés sur le centre et la circonférence. On donne l'aire A du carré rose, quelle est l'aire du carré bleu ? Exemple avec A = 100. Solution En vert sont matérialisés des rayons du cercle (r).

742. Triangle rectangle et cercles
Énigme Un triangle rectangle et deux cercles tangents internes. Longueur r du rayon ? Solution Via les aires des triangles:

743. Quart de cercle
Énigme Un quart de cercle de rayon 5. Un rectangle inscrit dont l'un des côtés vaut 3. Quelle est l'aire de la zone bleue ? Solution	Voir Énigmes avec rectangles

744. Rectangle et cercle
Problème Dans un rectangle, un triangle rectangle (12, 16) et un demi-cercle ayant l'hypoténuse pour diamètre. Quelle est l'aire de la zone bleue ? Solution Aire bleue = aire du carré – aire du triangle – aire du demi-cercle

745. Hexagone et carré
Problème Un pentagone et un carré ayant le même côté. Quelle est la valeur de l'angle alpha ?

746. Parallélogramme
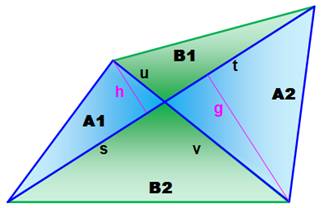
Énigme Un parallélogramme. Un point interne quelconque. Montrer que: aire (A1 + A2) = aire (B1 + B2). Solution On trace les parallèles aux côtés qui passent par le point (pointillés): création de quatre petits parallélogrammes. Les segments centre-sommets sont les diagonales de ces parallélogrammes et elles les divisent en deux triangles de même aire (même hauteur et même base). En combinant ces triangles deux à deux, on crée les triangles A1 et B1 d'une part et B1 et B2 d'autre part qui ont même aire totale.	Parallélogramme

747. Quadrilatère

Énigme

Un quadrilatère et ses diagonales.

Montrer que les produits des aires sont égaux: A1 ، A2 = B1 ، B2

Solution

On trace les hauteurs h et g des triangles.

Calcul de l'aire des triangles.

Application à une énigme virale Avec les valeurs indiquée, l'aire ocre vaut (3x2) / 1 = 6.
Autre énigme Est-il possible de trouver quatre aires de valeurs entières consécutives ? À l'évidence non !

Quadrilatère quelconque

Voir Quadrilatères et bimédianes

748. Quadrilatère circonscrit
Énigme Un quadrilatère circonscrit à un cercle (quadrilatère tangentiel). Montrer que: aire (A1 + A2) = aire (B1 + B2). Solution On trace les rayons vers les points de tangence. Ils sont perpendiculaires aux tangentes, donc aux côtes. Les deux segments issus d'un sommet vers les deux points de tangence sont de même longueur. De sorte que, les deux triangles partageant un même côté ont la même aire En combinant les triangles deux à deux, on obtient l'égalité cherchée.	Quadrilatère tangentiel

749. Carpette
Théorème de la carpette Si deux surfaces se croisent, une fois retirée la partie de chevauchement, les parties qui restent sur chacune des surface ont la même aire. Application dans le carré (Illustration) Ici, ce sont deux triangles qui se croisent. À gauche, chacune des deux parties colorées totalise: 80 + 13,33 = 93,33. À droite, plus subtil, on trouve bien: 106,67 = 20 + 20 + 66,67.		Cas d'un carré avec points mobiles au milieu des côtés Exemples numériques avec carré de 20x20
Pour en savoir plus	>>> Théorème de la carpette - Explications		>>> Brèves Géométrie – Index

750. Quart et demi-cercles
Énigme Un quart de cercle et un demi-cercle inscrit. Quel est le ratio entre les deux aires A (quart de cercle) et B (demi-cercle) ? Solution	.

751. Boomerang
Énigme Quelle l'aire de cette forme boomerang bleue, en fonction de l'aire S du demi-cercle rouge ? Les trois demi-cercles supérieurs ont le même rayon. Le demi-cercle inférieur a, par conséquent, un rayon égal à 3r. Solution	. Aire bleue = aire d'un cercle complet rouge

752. Carrés empilés
Énigme Trois carrés dont les côtés sont des nombres consécutifs, calculer l'aire de cette figure. Solution Côté des carrés: n – 1, n et n + 1. La figure du bas indique les dimensions qu'il est possible de noter. Homothétie dans le triangle: Longueur de l'hypoténuse: En égalant avec la consigne: Aire de la figure 5² + 6² + 7² - 1×2 = 108	.

753. Cube en équilibre
Énigme Calculer l'aire du carré bleu connaissant les aires indiquées pour les autres carrés. Tactique Calculer les dimensions des marches d'escaliers des trois cubes empilés. Le carré de gauche ne sert à rien sinon à caler la chute du grand carré. On note hi et vi la taille de chaque marche. Tableau de calcul	. Relations de calcul

754. Quel est l'angle ?
Énigme Un quadrilatère; trois côté égaux; un angle droit; un angle connu. Quelle est la valeur de l'angle alpha ? Tactique Tracé complémentaire faisant apparaitre un losange.
Solution

755. Isocèle en cercle
Énigme Un triangle isocèle ABC; Son cercle circonscrit de centre D; La bissectrice de l'angle en A; Intersection de BC en E; Segment DE. Quelle est la valeur de l'angle alpha ?
Tactique Construction d'un triangle équilatéral dont on démontrera que l'un des sommets est le point E, point d'intersection avec la bissectrice de l'angle en A. On fera grand usage du théorème de l'angle inscrit. Tracé Point F sur AC tel que AF = FD. Triangle équilatéral FDH. Il faut démontrer que les points H et E sont confondus.
Démonstration Démonstration d'après une idée d' Apostolis Manoloudis

756. Triangle dans rectangle
Énigme Un rectangle avec un triangle inscrit. En fonction des aires données, calculer l'aire w. Tactique Calculer les dimensions u et v avec les aires x et y, puis injecter ces valeurs dans le calcul de z.
Solution
Exemples de solution L'aire du rectangle est toujours égale à: Avec a = 5 alors b = 4,35959179… et u = 1,6 et v = 1,37627564…			Quelques autres solutions Il en existe une infinité

757. Les deux cercles
Énigme Un demi-cercle de diamètre AB = 10 cm. Segment AC = 8 cm. Perpendiculaire en C à AB. Intersection O'. Cercle (O', O'C). Intersections E et F. Quelle est la longueur t de EF ? Solution Dans le triangle rectangle OO'C, théorème de Pythagore: O'C (rayon du cercle) = 4 cm. Pointillés roses: deux triangles isocèles: les diagonales du cerf-volant sont orthogonales. Toujours avec Pythagore dans les triangles rectangles EHO et EHO': OH² = 5² – (t/2)² et O'H = 4² – (t/2)² Équation et sa résolution avec T = (t/2)²

758. Hexagone et triangles
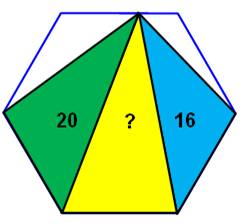
Énigme Un hexagone et les trois triangles colorés dont l'aire de deux d'entre eux est connue. Trouver l'aire du troisième. Tactique Ne pas passer par les calculs, mais exploiter une propriété peu connue des hexagones. Solution Avec A = aire de l'hexagone. Somme des aires des triangles vert et bleu, constante = A / 2. Aire du triangle jaune, constante = A / 3. Aire jaune = 2 x (20 + 16) / 3 = 24.	Note: cette figure est à l'échelle. Le côté mesure:

759. Triangle rectangle et carré

Énigme

Un triangle rectangle dont on connait l'hypoténuse.

Un carré inscrit dans l'angle droit de côté 12.

Quelles sont les dimensions x et y du triangle ?

Solution

Hypoténuse
Carré inscrit
Équation (A = x+y)
Racines
Racine positive
Équation
Solution

En nombre entiers !

21² + 28² = 35² est un triplet de Pythagore.

Solution numérique

x = 28, y = 21, a = 9, b = 16

Pour en savoir plus

>>> Brèves Énigmes – Index >>> Brèves Géométrie – Index

>>> Défis en géométrie – Index >>> Énigmes virales sur Internet

Retour	Brèves de maths – Page 37
Suite	Brèves de maths – Page 39 Défis mathématiques – Index SANGAKUS
Voir	Voir liens en haut de page Page miroir sur site parallèle
Cette page	http://villemin.gerard.free.fr/NombDico/aBreves/Breve38.htm