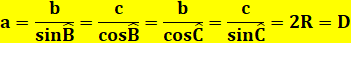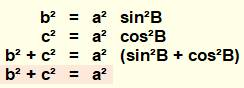|
Édition du: 25/12/2023 |
|
INDEX |
Triangles – Relations |
|||
![]()
|
Triangles – Loi des SINUS Belles
proportions entre les longueurs des côtés du triangle et les sinus de ses
angles.
|
||
|
|
Sommaire de cette page >>> Loi des sinus >>> Démonstration >>> Loi des sinus mariée à celle des cosinus >>> Triangle rectangle et Pythagore |
Débutants Glossaire |
|
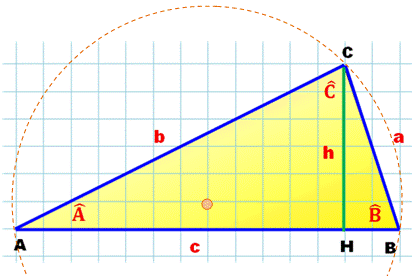
Triangle Un triangle
quelconque ABC. Notations usuelles des angles et des côtés. Son aire A. Son cercle
circonscrit de rayon R et diamètre D. Une des hauteurs
h. Loi des sinus
|
|
|
|
En 1670, Jean
Picard (1620-1682) mesure le degré de méridien terrestre. Cette formule est à
la base de ses calculs: le rapport d'un côté au sinus de l'angle opposé est
constant. Il obtient 57
057 toises soit 40 033 km pour la longueur du méridien. Valeur d'aujourd'hui: 40 007, 864 km Voir Denis Guedj / Sphère terrestre |
||
|
Démonstration via les hauteurs
|
Procédé La loi
des sinus n'est finalement qu'un moyen commode (et esthétique) de ne pas
reprendre le calcul via les hauteurs à chaque fois. Rappel
du calcul des proportions
|
|
|
Démonstration via le
calcul de l'aire (S) L'aire du
triangle peut s'exprimer de trois façons en prenant les trois hauteurs. La suite
consiste à multiplier ces expressions par 2 / abc. De la sorte, on obtient
également la valeur du rapport en fonction de l'aire. |
|
|
|
Valable pour deux autres identités par
permutations circulaire des angles. |
|
Voir Loi des cosinus
|
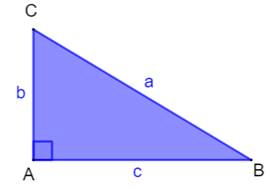
Triangle rectangle
La loi des sinus
devient:
On retrouve le fait que BC est un diamètre du
cercle circonscrit: a = 2R. On retrouve également le théorème
de Pythagore qui s'applique au triangle
rectangle en exprimant les carrés des côtés à partir de la loi des sinus.
Notons que la loi des
sinus a été démontrée sans le théorème de Pythagore. Ouf, on ne tourne pas en
rond ! |
Notations
Un angle droit en A et deux angles complémentaires en B et C. Théorème de Pythagore (immédiat !)
Rappel:
sin² + cos² = 1. |
|
|
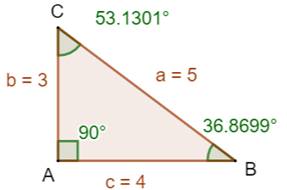
Application numérique Dans le triangle rectangle ABC
(3, 4, 5) Angle en B =
arctan (3/4) = 36,8698976458…
Sin B = cos C = 0,6
Sin C = cos B = 0,8 Loi des sinus 5
= 3 / 0,6 = 4 / 0,8 |
|
|
Voir Réciproque du
théorème de Pythagore avec la loi des cosinus
Voir
Démonstration
du théorème de Pythagore (loi des sinus) et sa réciproque par M. Gourine
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Triangle/Calcul/LoiSinus.htm
|