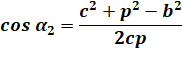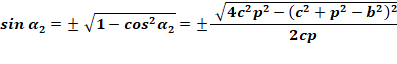|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
QUADRILATÈRE & SEGMENTS Longueur du sixième segment
Le quadrilatère est
caractérisé par la longueur de ses quatre
côtés et de ses deux diagonales. En fait,
seuls cinq de ces paramètres suffisent. Comment
calculer le sixième?
Dans un premier temps, on
étudie un quadrilatère complètement connu pour élaborer les formules et, dans
un second temps, on cherche l'inconnu. |
|
|
||
|
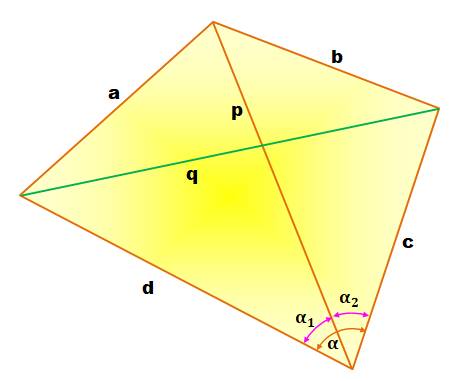
Un quadrilatère convexe
quelconque ABCD. Longueur des côtés: a, b, c
et d. Longueur des diagonales: p
et q. Connaissance du quadrilatère 1) Nous allons calculer la longueur des six segments en utilisant la figure
et le théorème de Pythagore. 2) Calcul de l'aire du quadrilatère par la méthode des triangles. Calcul du segment manquant 3) Méthode trigonométrique (loi des cosinus). 4) Méthode analytique (équations). 5) Méthode de résolution par approximations successives. |
|
|
|
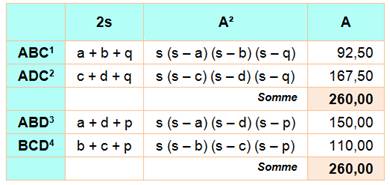
Tableau des valeurs (exemple) Par exemple pour calculer a, on compte 11 carreaux en x et 10 carreaux
en y. Alors: a² = 11² + 10² = 221 La valeur notée s est celle du demi-périmètre du quadrilatère On donne en bas du tableau, le résultat du calcul de l'aire du
quadrilatère selon deux méthodes: générale
et Bretschneider |
|
|
|
|
|||||
|
La
méthode consiste à évaluer q par l'angle alpha qui l'intercepte. C'est la loi
des cosinus (ou formules d'Al Kashi) qui va nous aider à trois reprises. Faisant
appel au calcul d'arc-cosinus, il n'est pas possible de donner une formule
littérale à la valeur de q. Nous allons effectuer les calculs avec les
chiffres de l'exemple précédent. |
|
||||
|
Avec l'angle alpha |
|
a = 14,866 b = 13,928 p = 21,541 c = 15,811 d = 21,471 q = ? |
|||
|
Avec l'angle alpha 1 |
|
|
|||
|
Avec l'angle alpha 2 |
|
|
|||
|
Avec l'angle alpha |
|
q²
= 600,9999… q = 24,515 |
|||
|
Détails du calcul Restart est une sécurité. Cette instruction
efface toutes les données dans les mémoires (= clear des calculettes). Les cinq premières lignes reprennent le calcul
des longueurs à partir des coordonnées de la figure. A1 est le cosinus de l'angle alpha1 et A11 la valeur
de l'angle en faisant appel à
l'arc-cosinus. Pour information, la valeur de l'angle en degré. A2 et A22 sont relatifs à l'angle alpha 2. L'angle alpha est la somme des deux. Q2 est le carré de la diagonale q dont on calcule
la racine carrée (square root). |
|
||||
Vers une formule algébrique complète
|
Expression des sinus |
|
|
Expression de q² |
|
|
Finalisation
|
|
|
Commentaires |
Il y a deux solutions, ce qui est normal, puisque les deux triangles a-d-p et b-c-p peuvent aussi être partiellement superposés. Si
l'on débarrasse cette relation des radicaux, et qu'on développe, on trouve un
polynôme de degré 6 en 6 variables, qui est le déterminant de Cayley-Menger,
relation entre les six distances de quatre points coplanaires. |
Merci à Patrick Pradeau pour m'avoir indiqué
cette méthode complète de calcul
|
|
||
|
L'aire du triangle
quelconque est égale à:
Nous allons nous en remettre à l'égalité des aires indiquée ici:
Tableau
de calculs
Nous retrouvons bien les valeurs précédente (260) pour la valeur de
l'aire. |
Avec le calcul de l'aire du quadrilatère par la somme des triangles,
nous disposons de deux évaluations; de
deux expressions égales. |
|
|
|
||
|
Supposons que q soit le fameux segment inconnu.
|
Dans l'équation A1 = A2, q
est la seule inconnue. En principe, sa valeur est calculable. Mais,
c'est horriblement compliqué. |
|
|
Le calcul conduit à: |
|
|
|
La résolution de A1 = A2 donne deux valeurs (outre
deux valeurs négatives). |
q = 25,51 celle que nous cherchons, et q' = 21,25 une valeur
artefact |
|
|
Commentaires Avec les diagonales p ou q
le calcul n'est pas simple, il est
encore plus compliqué pour l'un des côtés, car chacun participe à chacune des
évaluations de l'aire. |
L'artefact (solution non
désirée) est due au fait qu'il peut y avoir une inversion de l'un des quatre
triangles. Par exemple avec un retournement du triangle ACD, la quadrilatère
deviendrait ABCD'. |
|
|
|
|
|
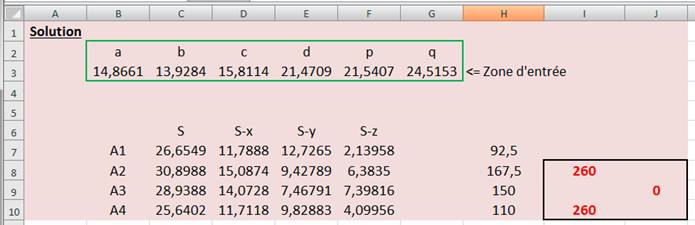
La méthode consiste à utilise un tableur. Avec une calculette, ce serait encore
fastidieux! Mieux un logiciel de calcul comme Maple. Une idée de disposition des calculs
Nous introduisons les cinq longueurs connues dans la zone d'entrée
(encadré vert). Puis, une valeur devinée dans la sixième case En rouge, l'évaluation des deux aires qui doivent être identique. Par ajustement de la valeur, obtenir l'écart le plus petit possible. Accès au tableur >>> Note: Pour faciliter l'encadrement, deux solutions sont implémentée. Les
deux résultats permettent de mieux apprécier la réduction de l'écart.
|
|
|
Calculer
la longueur d'un segment (côtés ou diagonales) d'un quadrilatère quelconque
est réalisable, connaissant les cinq autres. Les deux méthodes exposées ont
leur mérite. Dans les deux cas, une calculette scientifique ou un logiciel de
calcul sont nécessaires. |
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()