Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 01/11/2020 M'écrire Brèves de Maths

INDEX Types de triangles Triangle Géométrie	Triangle: Droites remarquables
	Droites et points	Bissectrices	Hauteurs – Propriétés
	Point Milieu	Médianes	Hauteurs – Démo
	Point et triangles	Médiatrices	Hauteurs – Démo-suite
	Distances

HAUTEURS du TRIANGLE (1/3) Quelques propriétés remarquables des hauteurs des triangles et l'orthocentre. On trouvera d'autres propriétés lors de l'exploration des démonstrations sur les pages suivantes.
	Sommaire de cette page >>> Propriétés – Longueurs et angles >>> Hauteurs et cercle circonscrit >>> Cercle de Taylor >>> Hauteurs et parallélogrammes >>> Distances aux sommets >>> Obtus ou aigus ? >>> Historique sur la connaissance de l'orthocentre >>> Anglais	Débutants Géométrie Glossaire Hauteur

Voir Propriétés fondamentales des triangles

Propriétés – Longueurs et angles

haut

Longueur de la hauteur

La hauteur AA' partage le triangle quelconque ABC en deux triangles rectangles.

Sa longueur h:

Propriété vraie pour chacune des trois hauteurs.

Angles avec les hauteurs

Un triangle quelconque et ses trois hauteurs.

Les deux triangles rectangles jaunes, opposés par un sommet, sont semblables:

Les angles A₁ et C₂ sont égaux.

Même chose pour les autres.

Propriétés sur les angles et les longueurs

Voir Démo par théorème de Ceva / Cosinus

Remarque

Cette propriété est indépendante du fait que les hauteurs sont concourantes. Elle pourra être utilisée pour le démontrer.

Voir Quadrilatères cocycliques

Théorème

AH.HA' = BH.HB' = CH.HC' = r² = 4R² – 1/2 (a²+b²+c²)

r est le rayon du cercle polaire du triangle ABC.

R est le rayon du cercle circonscrit.

Propriétés – Hauteurs et cercle circonscrit		haut
Propriétés de symétrie avec le cercle circonscrit Triangle ABC et son cercle circonscrit. Ses hauteurs AA', BB' et CC' prolongées: HA' = A'A'' HB' = B'B'' HC' = C'C'' Les demi-droites issues de H et joignant les milieux des côtés: HE = EE' HF = FF' HG = GG'

Propriétés – Cercle de Taylor		haut
Propriétés des projetés des pieds des hauteurs Triangle ABC et son cercle circonscrit. Ses hauteurs. Projection des pieds des hauteurs sue les côté du triangle. Les six points créés sont cocycliques. Le cercle bleu est le cercle de Taylor. L'hexagone est l'hexagone de Catalan. Les segments en pointillés orange sont égaux.

Propriétés – Hauteurs et parallélogrammes		haut
Parallélogramme avec les hauteurs Triangle ABC et son cercle circonscrit. Le point E diamétralement opposé à A0 Les triangles ABE et ACE sont inscrits dans un demi-cercle: ils sont rectangles. BE et CC', perpendiculaires à AB sont parallèles. CE et BB', perpendiculaires à AC sont parallèles. Avec des côtés parallèles deux à deux, le quadrilatère BECC' (bleu) est un parallélogramme.

Propriétés – Distances aux sommets		haut
Théorème h1² – h2² = a1² – a2² = c² – b² Vérification numérique (6² + 3²) – (4² + 3²) = 6² – 4² = (6² + 8²) – (4² + 8²) Démonstration Avec le théorème de Pythagore, on montre que: h1² = a1² + HA'² et h2² = a2² + HA'² h1² – h2² = a1² – a2² Comme cette égalité est vraie pour tout point de AA', elle l'est aussi pour le point A. Théorème Un point M se trouve sur la hauteur issue de A si et seulement si: MB² – MC² = AB² – AC².

Obtus ou aigu ?		haut
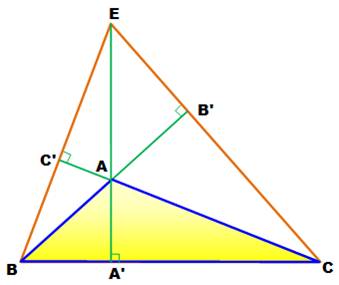
Les trois hauteurs se coupent en un même point. Ce point est l'orthocentre. L'orthocentre est interne au triangle s'il est acutangle et externe pour un obtusangle. Si H est l'orthocentre du triangle ABC, A est celui de BCH, B celui de ACH et C celui de ABH. Théorème Si les hauteurs sont concourantes pour un triangle acutangle, elles le sont pour un triangle obtusangle. Un triangle ABC et ses hauteurs en vert. On prolonge les segments BC' et CB' avec leur intersection en E. On dessine la hauteur EA' du triangle BCE. Passe-elle par A ? Si les hauteurs (EA', BB' et CC') du triangle acutangle BCE sont effectivement concourantes en A, alors les hauteurs (AA', BC' et CB') du triangle obtusangle ABC sont également concourantes(en E).

Historique sur la connaissance de l'orthocentre

Euclide – Les éléments: non mentionné.

Archimède – Livre des Lemmes: propriété et démonstration. Mentionné dans les commentaires sur ce livre, écrits par Nasrawi et attribués à al-Kuhi, un mathématicien médiéval du dixième siècle.

Moyen-âge: sans doute connu sans preuve (Pappus, Proclus, Regiomontanus, and Rudolph van Ceulen).

Vers 1750, première preuve connue par William Chapple (1718-1781).

Gauss est le créateur de la démonstration classique utilisant le triangle médian

English corner

Of all the traditional (or Greek) centers of a triangle, the orthocenter (i.e., the point of concurrence of the altitudes) is probably the one that attracted the most of attention.

The orthocenter of a triangle is de
fined to be the point of concurrence of the altitudes of the triangle.

SUITE page 2/3 >>>

Haut de page

Retour	Droites et points
Suite	Hauteurs – Démonstrations (2/3) Hauteur d'un triangle – Coordonnées de l'orthocentre Hauteur d'un triangle – Distances à l'orthocentre
Voir	DicoMot DicoNombre Droite de Simson Droite d'Euler Éléments de géométrie	Médianes Triangle – Débutants, novices Triangle – Glossaire Triangle – Index
Sites	Hauteur d'un triangle – Wikipédia Le concours des hauteurs d’un triangle – Daniel PERRIN – Université Paris Saclay Proof that the Altitudes of a Triangle are Concurrent – The University of Georgia Concurrency of the Altitudes of a Triangle – Mowaffaq Hajja and Horst Martini
Cette page	http://villemin.gerard.free.fr/GeomLAV/Triangle/Propriet/Hauteurs.htm