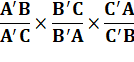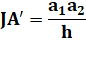Hauteurs dans le triangle - Démonstrations

Édition du: 01/11/2020

INDEX Types de triangles Triangle Géométrie	Triangle: Droites remarquables
	Droites et points	Bissectrices	Hauteurs – Propriétés
	Point Milieu	Médianes	Hauteurs – Démo
	Point et triangles	Médiatrices	Hauteurs – Démo-suite
	Distances

HAUTEURS du TRIANGLE (2/3)

Démonstrations de leur intersection en un point unique, l'orthocentre.

Occasion de découvrir de nombreuses propriétés des hauteurs des triangles.

Sommaire de cette page

>>> Types de démonstrations

>>> Démo de Gauss

>>> Démo avec le théorème de Ceva

>>> Démo avec trois cercles

>>> Démo de Newton

>>> Démo par les longueurs

Débutants

Géométrie

Glossaire

Hauteur

Voir Propriétés fondamentales des triangles

Types de démonstrations

Il existe plusieurs manières de démontrer que les hauteurs d'un triangle quelconque sont concourantes (Alexander Bogomolny en publie 22).

Une douzaine sur mes pages:

- Montrer que les longueurs satisfont un critère d'intersection unique

théorème de Ceva.

intersection des cordes de trois cercles

théorème de Carnot

- Montrer que les hauteurs s'apparentent à d'autres droites concourantes comme:

les médiatrices,

les bissectrices,

la hauteur symétrique.

- Montrer que les intersections des hauteurs deux à deux ont mêmes coordonnées:

méthode de Newton,

méthode des longueurs.

- Montrer que la droite qui passe par le point d'intersection de deux hauteurs est aussi une hauteur:

méthode des quadrilatères inscriptibles,

méthode de la droite parallèle à la hauteur,

méthode des vecteurs,

méthode des nombres complexes.

Voir Démonstrations du théorème de Pythagore

Démonstration de Gauss – La plus immédiate

haut

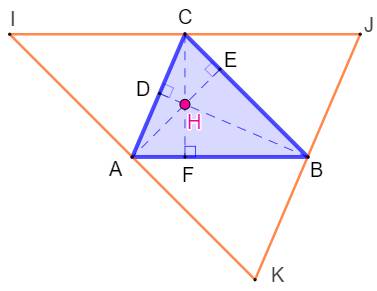
Démonstration classique – Le centre de cercle circonscrit est l'orthocentre du triangle médian

On construit le triangle IJK autour du triangle ABC, les côtés sont parallèles deux à deux et forment trois parallélogrammes: ABCI, ABJC et ACBK. Le triangle ABC est le triangle médian de IJK.

De ce fait, les points A, B et C sont les milieux des côtés de IJK, et les hauteurs de ABC sont les médiatrices de IJK.

Or, les médiatrices de IJK sont concourantes; les hauteurs de ABC le sont également.

Les médiatrices sont concourantes car, si l'on prend l'intersection H de deux d'entre elles (HA et HB), ce point est à égale distance des sommets: HI = HK et HK = HJ. Avec HI = HJ, ce point est aussi sur la troisième médiatrice HC.

Hauteurs et médiatrices à la fois

Avec les parallélogrammes: AB = IC = CJ; Le point C est le milieu de IJ

CF est perpendiculaire en F à AB; IJ est parallèle à AB; CF est perpendiculaire en Cà IJ. Alors, CF, hauteur de ABC, est aussi une médiatrice de IJK.

Démonstration avec le théorème de Ceva

haut

Le théorème de Ceva est une condition nécessaire et suffisante pour que trois céviennes soient concourantes:

Avec les cosinus des angles aux sommets du triangle

Voir Théorème des perpendiculaires concourantes

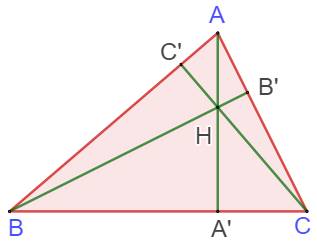
Démonstration avec le théorème de Carnot

haut

Théorème de Carnot

Avec cette figure, le théorème de Carnot dit que pour tout point P:

BA'² – A'C² + CB'² – B'A² + AC'² – C'B² = 0

Dans le cas des hauteurs:
AB² – BA'² = AA'² = AC² – CA'²
Induit: BA'² – CA'² = AB² – AC²
De même: AC'² – BC'² = AC² – BC²
Et: CB'² – AB'² = BC² – AB²

L'égalité devient celle du théorème. Dans ce cas, le point P est bien le point H, point de concours des hauteurs.

Démonstration avec trois cercles

haut

Théorème des trois cordes – Gaspard Monge

Les cordes formées par trois cercles sécants se coupent en un point unique.

Dessinons donc trois cercles ayant pour diamètre les côtés du triangle ABC. Intersections en A', B' et C'.

Selon le théorème, les cordes AA', BB', CC' se coupent en un point unique H.

Or, les triangles comme AA'B, inscrits dans un demi-cercle sont rectangles. Donc l'angle en A' est un angle droit et AA' est une hauteur du triangle ABC.

Idem pour les deux autres. H est l'orthocentre.

Démonstration de Newton

haut

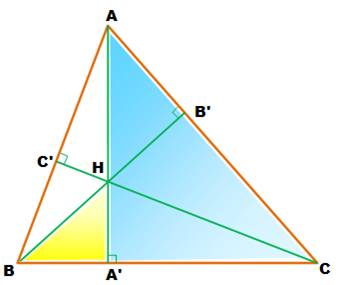
Les deux triangles colorés sont semblables.

Si H est l'intersection des hauteurs AA' et BB':

Si G est l'intersection des hauteurs AA' et CC':

Donc: HA' = GA' et les points H et G sont confondus. Les trois hauteurs sont concourantes.

Démonstration par les longueurs		haut
Démonstration par test sur les coordonnées L'idée consiste à supposer que les trois hauteurs se coupent deux à deux en trois points (I, J et K), et à monter que ces trois points sont confondus. Sachant que J et K sont sur la même droite, il suffit de montrer qu'ils ont la même distance au point A' pour prouver qu'ils sont confondus: JA' = KA' ?
On évalue séparément la longueur des deux segments.
Or, on sait que (aussi: triangles semblables vus ci-dessus): B₂ = A₂ et C₂ = A₁
Valeur des tangentes:
Conclusion avec JA' = KA':	Les points J et K sont confondus. Même démonstration pour les deux autres couples.

Cette démonstration m'a été signalée par Rachid Ranouaoui

Variante avec proportionnalités

Du fait de l'égalité des angles, les triangles AA'B et CA'K sont semblables
et A'B . A'C = A'A . A'K.

Avec les triangles semblables AA'C et BA'J, on a aussi: A'B . A'C = A'A . A'J.

Ce qui entraine: A'K = A'J. Les points K et J sont confondus.

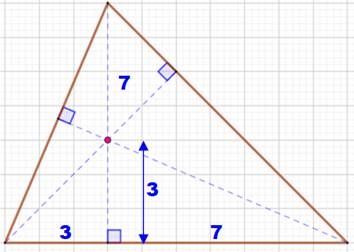
Propriété

Distance à l'orthocentre H:

Exemple

a₁ = 3, a₂ = 7 et ha = 7

Distance à l'orthocentre HA':

3 x 7 / 7 = 3

b₁ = 2,83, b₂ = 7,07 et hb = 7,07

Distance à l'orthocentre HB':

2,83 x 7,07 / 7,07 = 2,83

c₁ = 3,68, c₂ = 3,94 et hc = 9,19

Distance à l'orthocentre HC':

3,68 x 3,94 / 9,19 = 1,58

SUITE page 3/3 >>>

Haut de page

Retour	Droites et points Hauteurs – Propriétés (1/3)
Suite	Hauteurs – Démonstrations – Suite (3/3) Médianes Droite d'Euler Droite de Simson
Voir	Triangle – Index Triangle – Glossaire Éléments de géométrie Triangle – Débutants, novices DicoMot DicoNombre
Sites	Le concours des hauteurs d’un triangle – Daniel PERRIN – Université Paris Saclay Existence of the Orthocenter – Cut-the-Knot – Alexander Bogomolny – Revue de 22 démonstrations Proof that the Altitudes of a Triangle are Concurrent – The University of Georgia Concurrency of the Altitudes of a Triangle – Mowaffaq Hajja and Horst Martini
Cette page	http://villemin.gerard.free.fr/GeomLAV/Triangle/Propriet/Hauteur1.htm