|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
TRIANGLE et DROITES de partage Voici trois théorèmes
importants concernant des droites de partage dans le triangle. Avec
démonstrations. En prime la démonstration du joli théorème des
parallélogrammes liant les côtés et les diagonales. |
|
|
|||
|
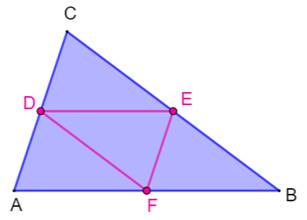
Le segment qui joint les milieux de deux côtés d'un triangle:
AB // A'B' [AB] = 2 [A'B'] Anglais The straight line connecting midpoints of two sides of a triangle:
|
|
||
|
Conséquence pour le triangle Les points D, E et F sont les
milieux des côtés. Les quatre petits triangles sont isométriques
et homothétiques au grand triangle dans un rapport 1/2. Les deux parallélogrammes ADEF et
BEDF sont isométriques et ont la même aire, égale à la moitié de celle du
grand triangle.
|
Les droites qui passent par les
points milieux sont parallèles au troisième côté. |
||
Voir Trapèze
Thalès
|
D'une
manière générale le théorème de
Thalès affirme que: dans un triangle, une parallèle à un côté engendre
des proportinalités et réciproquement. Dans le cas du point milieu, la
proportionalié est égale à ½. |
|
|
|||
|
Données
Ce qu'il faut démontrer
Démarche
|
On note que D est le symétrique de B' par
rapport à A'. Et aussi que les quadrilatères ABB'D et AB'CD sont des
parallélogrammes. |
||
|
Intuition?
Comment avoir l'idée de
dessiner ce point qui va faire apparître deux parallélogrammes ayant un côté
commun(AD)? Intéressant car de la connaissance des mesures de l'un on
rebondira pour connaître les mesures de l'autre. C'est l'intuition, nourrie
par une bonne connaissance des propriétés des objets et déclenchée par les
suggestions que nous délivent la lecture de la figure. Ici, droites
parallèles nous amène à parallélogramme. |
|||
|
Démonstration (niveau
collège)
|
A'C = A'A Angles: A3 = A4 Angles: A1 = A2 |
||
|
Outil: cas de congruence des triangles Deux
triangles ayant un côté de même longueur et deux angles égaux sont congrus (ou égaux). |
Triangles: T1 = T2 |
||
|
|
CB' = AD |
||
|
|
CB'
= BB' = AD BB'
// AD |
||
|
Outil: caractérisation d'un parallélogramme Si un quadrilatère (non croisé) a
deux côtés opposés parallèles et de même longueur, c'est un parallélogramme. |
ABB'D est un parallélogramme |
||
|
|
AB = DB' AB // DB' |
||
|
|
A'D = A'B' AB = DB' =
2A'B'
|
||
|
|
||
|
Un des médianes CM Le théorème de la médiane dit: a² + b² = 2 (m² + d²) ou a² + b² = 2 m² + ½ c² Anglais
Note:
bisect : qui coupe en deux (pas forcément en parts égales). |
|
|
Voir Démonstration / Aires des triangles sous
médiane
|
|
|||
|
Données
Ce qu'il faut démontrer a² + b² = 2 (m² + d²) Démarche
Calcul des longueurs en
utilisant le théorème de Pythagore. Démonstration |
|
||
|
Pythagore à l'oeuvre |
MC² = (x – 0)² + (y – 0)² = x² + y² = m² AC² = (x + d)² + (y – 0)² = x² + 2xd + d² + y² = b² BC² = (x – d)² + (y – 0)² = x² – 2xd + d² + y² = a² |
||
|
Somme des deux dernières |
a² + b² = 2x²+ 2d² + 2y² = 2
(x² + y² + d²) |
||
|
En remplaçant |
a² + b² = 2 (m² + d²)
|
||
|
|
||
|
a² + b² = 2 (m² + d²)
2a² + 2b² = 4m² + 4d² = 4(d1 / 2) ² + 4(d2 / 2) ² = d12 + d22 Règle (en
fait théorème) Dans un parallélogramme,
la somme des carrés des côtés est égale à la somme des carrés des diagonales. |
|
|
Voir Règle du parallélogramme
illustrée / Règle du parallélépipède
|
|
||
|
Généralisation du théorème de la
médiane à un point quelconque du troisième côté; autrement dit à toute cévienne. a²d + b²d' = c (m²
+ dd') Notez que: le dernier terme cdd' est un nombre entier. |
|
|
|
Un triangle quelconque ABC avec BC =
3 unités Un point D sur BC tel que BD = 2 unités. Calculer AC² + 2AB² – 3AD. Notre théorème s'écrit: 1 x AC² + 2 x AB² = 3 (AD² + 1
x 2) AC² + 2 AB² = 3AD² + 6 AC²
+ 2 AB² – 3AD² = 6 Un application simple qui montre que
cdd' = 3 x 2 x 1 = 6 est un nombre
entier. |
|
|
Voir Démonstration
|
Construction Un
triangle quelconque ABC. Deux
cercles tangents entre eux et chacun tangent à deux côtés du triangle. Quelle
est la longueur t de la tangente interne CD
? Pistes Pour
connaitre la longueur de CD, le théorème de Stewart est demandé. Les
segments issus d'un point quelconque et joignant les points
de tangence ont même longueur. Les
notations u, v, w et z reflètent ces égalités. |
|
|
|
Calculs
Calcul du rayon des cercles
Illustration
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Voir Démonstration (la même avec
vérification GeoGebra)
![]()
![]()