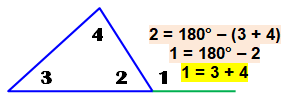NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 07/02/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	HISTOIRE – Géométrie
Débutants Général	CONSTRUCTIONS			Glossaire Général
INDEX Constructions Géométrie Histoire	Introduction	Duplication du cube	Trisection de l'angle
		Quadrature du cercle	Heptagone
		Sommaire de cette page >>> Trisection de l'angle droit et de l'angle plat >>> Bissection de l'angle >>> Équation pour la trisection >>> Construction à l'équerre >>> Construction avec règle et marques (neusis) >>> Constructions imaginées par Archimède puis Ceva >>> Construction de l'angle triple >>> Théorème de Marion Walter

La trisection de l'angle

Un des trois célèbres problèmes de construction de l'Antiquité.

La construction est réalisée avec règle sans graduation et compas uniquement. En général, la construction est impossible, sauf pour quelques angles particuliers comme 180°, 90° … (accessible à travers le tracé de l'hexagone)

Historique

Problème posé par Hippias d'Élis (-443 à -399), connu pour sa grand capacité de mémorisation.

Archimède (vers -450) propose une méthode par alignement.

Ceva (vers 1700) construit deux appareils mécaniques permettant la trisection par alignement.

En 1837, Wantzel (1814-1848) à montré que ce problème est insoluble.

Trisection de l'angle droit et de l'angle plat		haut
Possible ! La trisection de l'angle droit, comme de l'angle plat, est possible à la règle et au compas. Construction pour l'angle droit Angle droit AOB. Un cercle de centre O, de rayon quelconque qui coupe l'angle en A et B. Médiatrices des segments OA et OB. Les points d'intersection M et N avec le cercle permettent de tracer les demi-droites en vert (OM et ON) qui découpent l'angle droit en trois angles de 30°. Cette construction exploite le fait que: cos(30°) = sin(60°) = 1/2.	La trisection de l'angle plat est obtenue avec la demi-droite ON et sa symétrique OP par rapport à OB.

Voir Construction – Index

BISSECTION DE L'ANGLE – Rappel
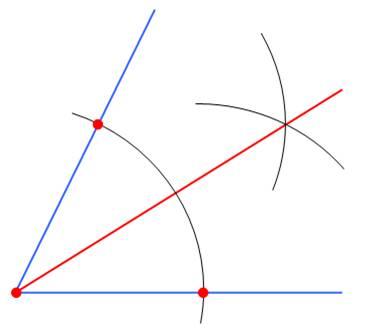
Comment partager un angle en deux angles égaux. La demi-droite qui partage l'angle est la bissectrice Cette opération est classique et très facile à réaliser avec un compas. Du sommet de l'angle, tracez un cercle. à partir de chacun des points d'intersection dessinez un cercle identique (qui peut être différent du tout premier).

Suite en Bissection

Équation pour la trisection
Comment partager un angle en trois angles égaux. Là, la difficulté est très grande. Voici une idée de la démonstration en faisant l'hypothèse d'un angle de 20°
Calculons en général	cos(3a)	= cos(a) cos(2a) – sin(a) sin(2a)
		= cos(a) (cos^2(a) – sin^2(a)) – 2sin^2(a) cos(a)
		= cos(a) (2cos^2(a) – 1) – 2(1 – cos^2(a)) cos(a)
C'est la relation de l'angle triple		= 4cos^3(a) – 3cos(a)
Prenons le cas particulier de	a	= 20^o
	cos(3a)	= cos(60^o) = 1/2
L'équation, dans ce cas, devient	1/2	= 4cos^3(a) – 3cos(a)
	0	= 8cos^3(a) – 6cos(a) – 1
En remplaçant	cos(a)	= x
	0	= 8x^3 – 6x – 1
Soit l'équation, avec v = 2x	0	= v^3 – 3v – 1

Solution de l'équation ?
On cherche à savoir si les racines de cette équation sont rationnelles. Démonstration en 1837 par Pierre Laurent Wantzel (1814-1848).
Supposons que Oui, alors	v	= p/q fraction minimale (simplifiée)
En remplaçant dans l'équation	0	= (p/q)^3 – 3(p/q) – 1
En multipliant par q3	0	= p^3 – 3pq^2 – q^3
En reformulant	q^3	= p^3 – 3pq^2
		= p (p² – 3q²)
On déduit que	p est	divisible par q^3
Conséquence	p est	divisible par q
Impossible	p/q	est une fraction irréductible par hypothèse
Et en factorisant avec p3	p^3	=  3pq^2 + q^3
		= q (3p + q²)
On déduit que	q est	divisible par p^3
Conséquence	q est	divisible par p
Impossible	p/q	est une fraction irréductible par hypothèse
La supposition est fausse	v n'est par rationnel

Voir Constructions avec règle et compas

CONSTRUCTION avec ÉQUERRE seule
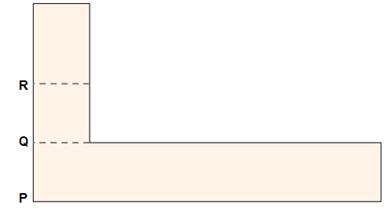
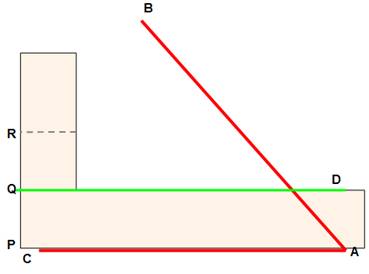
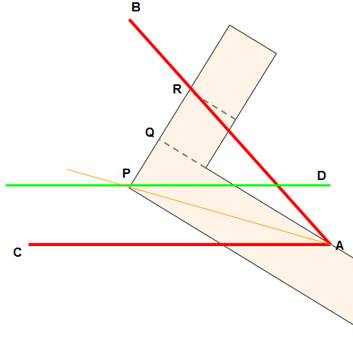
La construction à la règle et au compas n'est donc pas possible. Mais, voici une construction assez pratique. 1) Posez des repères sur l'équerre On marque Q en prolongement du bord intérieur et R tel que PQ = QR. 2) Préparation L'angle à partager en trois est l'angle BAC (on note BAC ). On construit la droite D. 3) Trisection On oriente l'équerre pour avoir: A sur le bord de l'équerre, P sur la droite D, et R sur la droite AB. Alors: CAP = PAQ = QAR = 1/3 CAB Note: Il existe aussi une CONSTRUCTION avec Conchoïde de Nicodème. Elle est plus compliquée et assez théorique.

Voir Équerre

CONSTRUCTION avec règle et marques (NEUSIS)
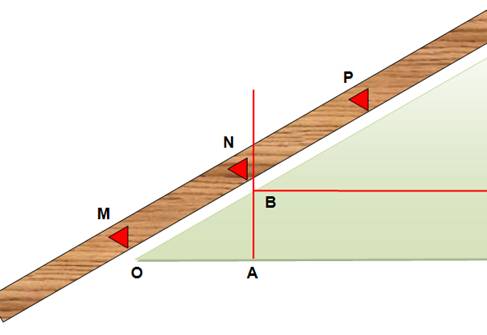
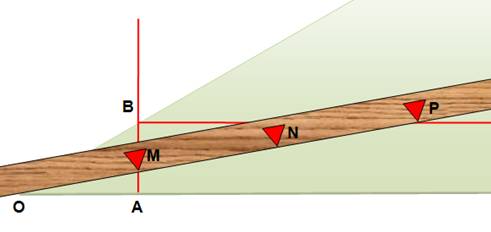
On autorise l'utilisation d'une règle sur laquelle il est possible de porter des marques. L'angle à partager en trois est AOB. En A, perpendiculaire à OA. En B, parallèle à OA. Sur la règle, on porte les marques M, N et P telles que MN = NP = OB. La règle est déplacée de façon telle que: M est sur AB, P est sur la parallèle en B, et la règle passe par O.
Cette méthode qui consiste à ajuster au mieux la règle sur les points désignés s'appelle neusis. Méthode très utilisée par les mathématiciens grecs. Ce mot en grec signifie: incliné vers.

Constructions imaginées par Archimède puis Ceva			haut
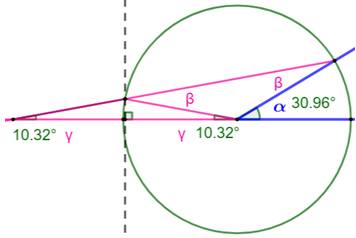
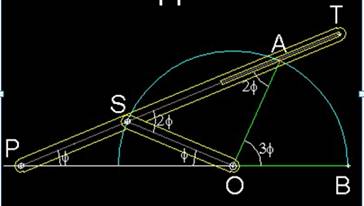
Principe Archimède imagine cette figure pour réaliser la trisection de l'angle. Rappel (les nombres 1, 2, 3 et 4 symbolisent les angles) Explications Dans le grand triangle: Dans le petit triangle rose: Soit la valeur d'alpha:
Pantographes de Ceva Tommaso Ceva (1648-1737), frère de Giovanni Ceva (1647-1734), auteur du fameux théorème. Il imagine cet instrument pour la trisection de l'angle AOB. Le point O est fixe. Le point P coulisse le long de PO. Les points R et S coulissent sur le cercle. Quatre bras de même longueur: PR = PS = OR = OS. La trisection est obtenue lorsque les bras PR et PS sont respectivement alignés avec RA et SB.
Ceva imagine également cet instrument pour construire l'angle SPO qui vaut le tiers de AOB. Les bras SP et SO sont de même longueur. Les points S et A coulissent sur un cercle. Le point O est fixe.

Source images des pantographes: Trisection using mechanicla links – Takaya Iwamoto

Voir Brève 53-1052

Construction de l'angle triple
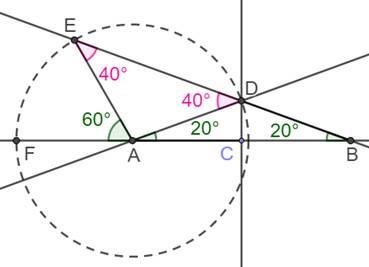
Construction Soit un angle entre deux droites (ici, celles qui vont porter les points A, B et D). Construire l'angle triple. Marquer les points A et C quelconques sur une des droites. Avec un cercle de centre C et de rayon CA, marquez le point B sur la droite AB (CA = CB). Dressez la perpendiculaire en C qui coupe la droite AD en D (CD est médiatrice de AB) Dessinez le cercle AD de centre A. La droite BD le coupe en E L'angle FAE est le triple de l'angle BAD. Démonstration Le triangle ABD est isocèle par construction, l'angle au sommet vaut 180 – 2a avec a l'angle à la base. Angle ADE = 180 – (180 – 2a) = 2a Le triangle AED est isocèle (AE = AD = R) Angle EAD = 180 – 2 (2a) = 180 – 4a Angle FAE = 180 – (180 – 4a – a) = 3a	Notez La construction du tiers d'angle est impossible; celle du triple est assez simple. Illustration Les triangles ABD et ADE sont isocèles
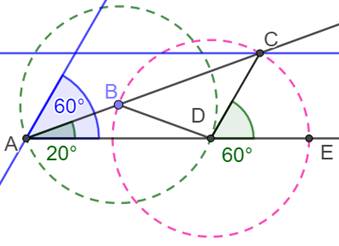
Construction semblable Dessinez l'angle (ici de 20°). Sommet A et un point quelconque B. Cercle de centre B et de rayon AB, coupe l'autre côté de l'angle en D. Cercle de centre D et de rayon DB, coupe le premier côté de l'angle en C. L'angle CDE est le triple de l'angle BAD. Les deux parallèles dessinées en bleu permettent de ramener l'angle triple sur l'angle initial. La démonstration est identique à celle présentée ci-dessus.	Brève 376

Théorème de Marion Walter – 1993
Les trisectrices d'un triangle délimitent un hexagone interne dont l'aire est 1/10 de celle du triangle. Marion Walter (1928-2021) est une mathématicienne allemande. Avec une division des côtés par 4, on obtient un hexagone dont l'aire vaut 8/35 fois celle du triangle – Luca Goldoni

Voir Brève 53-1051

Suite	Quadrature du cercle Trisection de l'angle de 90° Trisection du carré Trisection du carré par des paraboles	Trisection du rectangle Trisection du segment Trisection du quadrilatère Voir haut de page
Voir	Angle Bissection des triangles Géométrie – Index Hilbert	Premiers de Pierpont Règle et compas Transcendant
Sites	Trisection de l'angle – Wikipédia La trisection de l'angle – Descartes et les Mathématiques Trisection de l'angle selon Thomas Ceva Serge MEHL La trisection de l'angle – Études mathématiques – Outils Ces problèmes qui font les mathématiques – La trisection de l'angle – Jean Aymes – pdf 100 pages Trisection de l'angle à la règle et au compas* – Jean Jacquelin Panoplie du constructible* Pierre Delezoïde - Lycée Buffon - Paris XV Angle trisection – Wikimedia commons - Liste de toutes les méthodes de trisection de l'angle (79) Angle Trisection – Wolfram MathWorld Trisecting an angle – Mac Tutor An Interesting Example of Angle Trisection by Paperfolding – Sidney H. Kung – Cut-the-Knot
Livre	Le Dictionnaire Penguin des curiosités géométriques – David Wells - Eyrolles
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Histoire/Trisangl.htm