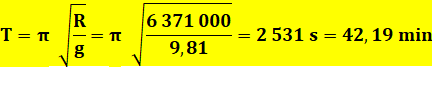|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
GRAVITATION Découverte et curiosités La traversée de la TERRE
Quelques notions amusantes
sur l'effet de la gravitation universelle. Parmi elles, comment se comporte une
balle lâchée dans un tunnel profond qui traverserait toute la Terre. Elle
jouerait indéfiniment au yoyo à la manière d'un pendule. Assez étrangement, la durée
de traversée de la Terre serait de 42 minutes et quelques secondes, même sans
passer par le centre de la Terre, et cela pour toutes sortes de balles ou
d'objets, comme un train. Un
super-moyen de locomotion pour aller, par exemple, de France en
Nouvelle-Calédonie en un temps record. Une belle idée mais irréalisable, bien
sûr. |
|
|
|||
|
Loi de la Gravité Tous les objets, quelle
que soit leur masse, lâchés de la même hauteur tombent par terre au même
moment. Voir Pesanteur Autre formulation L’accélération d’un objet en chute
libre, due à la pesanteur, est la même pour tous les objets. Voir Gravitation / Pesanteur Expérience de Galilée Tour
de Pise par Galilée: il lâche trois
balles d’acier de masses différentes du haut de la tour. Elles arrivent
toutes les trois en même temps au sol. Expérience de Robert Boyle Il retire l’air d’un récipient
contenant une balle d’acier et une plume. En renversant le récipient les deux
objets atteignent l’autre côté en même temps. Expérience de la pièce de monnaie Prenez une pièce de monnaie (ou un
morceau plat de métal). Une feuille de papier de même taille exactement (qui
ne dépasse pas). Si l’accélération avait été
différente, le papier aurait été ralenti. Expérience du pendule Soit un pendule formé d’un fil et
d’une masse.
|
|||
|
|
|
|
La Terre tourne autour du Soleil
Rotation de la Terre Supposons que nous puissions
augmenter la vitesse de rotation de la Terre à volonté. Nous sommes sur une
balance à l’équateur. Que se passe-t-il ? Réponse Le poids diminue lorsque la Terre
accélère. À une certaine vitesse dite critique,
la force centrifuge nécessaire pour nous conserver sur une trajectoire
circulaire égale la force gravitationnelle de la Terre. L’homme géant Un homme géant est placé sur
l’équateur. Il est vraiment très géant, il mesure 72 000 km. Que se
passe-t-il ? Réponse Son poids est nul ! Son centre de gravité est en
orbite |
|
|
|
|||||||||||||||||||||||||||||||||||||
|
Expérience mentale du centre de la Terre On creuse un trou de part en part de
la Terre.
Tableau de
progression
Liaison de ville à ville (train gravitationnel) Sur le même principe on creuse un
tunnel rectiligne entre les deux villes à relier.
Le milieu O est plus près du centre
C de la Terre que ne le sont les points A et B. Le train, partant
de A descend en accélérant vers O et remonte en décélérant vers B. Non
seulement ça marche, mais le mouvement est perpétuel en ignorant les
frictions. Record de saut sur la Lune La gravité sur la Lune
est 6 fois moins forte que sur la Terre. On y est six fois moins lourd. Un objet lancé avec une même force,
monte six fois plus haut. Je saute 2 m en hauteur sur la Terre. Quelle est ma
performance sur la lune ? Non, pas 12 m ! Mais vous avez dit … Réponse En fait, il faut calculer le
déplacement de mon centre de gravité. Mon centre de gravité se trouve à 1,2 m
du sol. |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
Au Moyen Âge l'idée de creuser un puits à
travers la Terre existait déjà. Contrairement à
l'idée de voler, celle-ci n'eut aucune suite. En 1632, Galilée
soutenait qu'un boulet de
canon lancée dans un tunnel traversant la Terre aurait un mouvement
harmonique simple, oscillant entre le côté de la Terre d'où elle a été lancée
et son point de sortie de l'autre côté de la Terre. Au XVIIe siècle, le
scientifique britannique Robert Hooke
écrit une lettre à Isaac Newton. Il a
l'idée d'un objet accélérant à l'intérieur d'un tunnel dans la Terre ou une
planète. Il avait calculé que le voyage à travers la Terre durerait moins de
trois-quarts d'heures. Newton pensait qu'un ballon lancé par un tunnel percé
à l'Équateur suivrait une trajectoire en spirale sous l'effet de la rotation
de la Terre. Newton
montre que la force de gravitation à l'intérieur de la Terre est
directement proportionnelle à
la distance au centre
de la Terre. Le voyageur arrivé à
mi-distance entre la
surface et le
centre ne pèse
plus que la moitié de son poids habituel. Au centre, il ne pèse plus
rien. >>> En 1966, Paul Cooper publie un article
dans the American Journal of Physics proposant un train gravitationnel comme
moyen de transport futur. Ce texte suscite de nombreux commentaires,
notamment sur l'allure de la trajectoire: linéaire ou brachistochrone. Courbe
brachistochrone: courbe dans un plan
vertical sur laquelle un point matériel pesant placé dans un champ de
pesanteur uniforme, glissant sans frottement et sans vitesse initiale,
présente un temps de parcours minimal parmi toutes les courbes joignant deux
points fixés. En 2004, Ivars Peterson relate les idées
de Galilée et relance la réflexion sur cette curiosité du tunnel
gravitationnel. D'autres (dont Alexander
Klotz) refont les calculs avec les moyens modernes et en tenant compte de
la nature des couches de la Terre. Faisabilité:Il est clair que cette idée est
irréalisable, même à faible profondeur. Faisabilité physique, coût sans
compter avec la force de déviation latérale de Coriolis qui ferait que le
train heurterait les parois. Rappels: coût du tunnel sous la Manche: 300 millions
de dollars par kilomètre (15 milliards pour 37 km de voies (50,5 km au total)
à 45 mètres sous terre). La mine la plus profonde se trouve à 3,6
km à comparer au 6 371 km pour atteindre le centre de la Terre. |
|
![]()
|
|
||
|
Tunnel gravitationnel: lâché de balle ou circulation d'un véhicule,
d'un train. Retour aux explications Données
|
|
|
|
Deux lois utiles (Newton):
|
La force de gravité pour une sphère homogène:
|
|
|
Calcul
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Données numériques |
G
= 6,67428 10-11 m3
kg-1 s-2 >>>
R
= 6 371 km |
|
|
|
|
|
|
|
Vitesse et gravité
|
De l'ordre de trente fois la
vitesse d'un
avion en altitude de croisière. |
|
d est la
distance à partir du sol (d = R – r). |
Pour d = 0, alors g = g0,
la gravitation en surface (9,81 m/s²); Pour d = R, alors g = 0; Pour d = R/2, alors g = ½ g0. |
|
Gravité le long d'un tunnel passant
par le centre de la Terre avec graphe de g = f(r)
|
|
Voir Courbe tenant compte de la densité
non-homgène de la terre en Free-fall acceleration sur Wikipedia (Anglais)
Miniature

|
Effet de la densité
|
Par compte, elle est fonction de la densité de la
planète. |
|
|
Tdensité moyenne = 42,2 min Tdensité réelle = 38 à 42,2 min |
|
Trajectoire
|
Peu de différence en fait. Mais des
calculs autrement plus compliqués. |
|
Curiosités
|
Période du satellite = Période de la balle |
|
|
Période sur D = Période sur ½ D |
Anglais:
Gravity Train, gravity express, gravity sled, gravity tunnel, tube travelling,
Journey
through the center of the Earth
![]()
|
Suite |
|
|
Voiir |
|
|
DicoNombre |
|
|
|
|
|
Cette page |
![]()