|
||||||||||||||||||||||||||||||||
![]()
|
Carré magique 4 x 4 Inclusion d'une date anniversaire Comment s'y prendre pour inclure une
date anniversaire (ou autre) dans un carré magique de 4 x 4 ? Avec les formules de Sallow et un tableur, c'est
souvent réalisable. Les impossibilités sont assez vite détectées. |
|
|
||
|
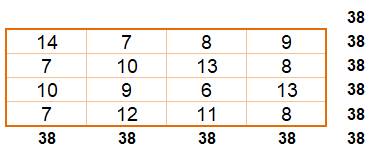
Avec ce
carré la date est sur la première ligne sous la forme: jour / mois / dizaine
de l'année / unité de l'année. NB. Dans ces
conditions, la suite des nombres de 1 à n² n'est pas respectée; même, il y a
des doublons. La constante est égale à
la somme des quatre nombres. |
Générique
Exemple avec l e14 juillet (17)89
|
|
Voir Date de
naissance en carré magique 3x3
|
|
||
|
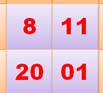
Réaliser
un carré 4x4 avec un carré 2x2 donnant la date anniversaire (exemple: le 8
novembre 2001) sous la forme indiquée. Idéalement,
ce carré sera placé au centre. Par
ailleurs, il serait souhaitable que la somme magique reflète le département
de naissance (33) ou alors celui de ma résidence (88). Est-ce
réalisable ? Note: contrairement au carré magique classique, les
nombres ne seront pas en continuité de 1 à n². |
|
|
Voir Comment construire un carré magique de constante donnée
|
|
||
|
La somme
magique d'un tel carré est imposée par le carré central: 8 + 11 + 20 + 1 =
40. Donc ni 33, ni 88, avec cette disposition. Le carré
magique, avec le carré-anniversaire au centre, n'est pas possible du fait de
la faible valeur du 1. Celle-ci impose des valeurs négatives sur d'autres
cellules. Le tableau
montre une solution, mais avec trois valeurs négatives. |
Impossible
|
|
|
Pour
éviter les valeurs négatives et obtenir la somme désirée, il faut changer la
place du carré-anniversaire. Nous allons le descendre d'un cran vers le bas. Du fait
des valeurs imposées pour la date anniversaire, la somme sera supérieure à 33
(les formules l'imposent). Nous allons viser 88. |
Carré visé
|
|
|
|
|||||||||||||||||||
|
Le tableur est utilisé comme une ardoise
et une aide au calculs. Les formules de Sallow sont utilisées. Elles nécessitent
de préciser la valeur de huit paramètres. Mais nous
avons quatre contraintes avec les quatre cellules anniversaires (rouges). La somme magique vaut: Pour atteindre S = 88: |
Formules de Sallow
Quatre valeurs imposées C = 8 et D = 1 A + c = 20 et B + c = 11 Conditions sur c et
les autres Si B = 1 alors c < 11. Avec A > 0, alors c > - 20 A varie de 1 à 30 et B de – 9 à 21 Avec B – d > 0, B > d Avec D + a – d, a > d – 1 |
||||||||||||||||||
|
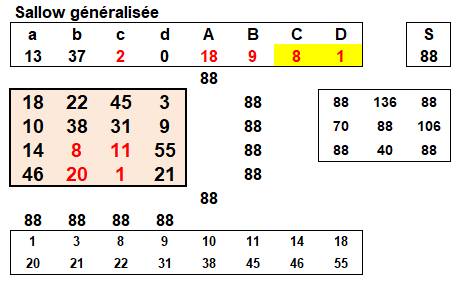
Disposition tableur En haut, les valeurs des paramètres. En rouge les
valeurs contraintes. Les paramètres a et b sont ajustés pour obtenir S = 88. Le carré magique, muni de ses formules, se
remplit automatiquement. Pour se rassurer, les dix sommes sont calculées
(88). En bas, l'énumération des 16 nombres utilisés
pour vérifier l'unicité de chacun. Les solutions sont trouvées après essais successifs. |
|
||||||||||||||||||
Une des solutions

|
|
||
|
Programmation Maple Initialisation et compteur de succès à zéro. Déclaration d'une matrice 4x4 Valeur connue pour C et DD (D est réservé à
Maple). Boucles
sur c et calcul de A et B. Boucles sur a, b et d. |
Vérifications Unicité des nombres dans la matrice
(ici, il s'agit d'un simple tableau à remplir): création de l'ensemble (set) des valeurs. La quantité (nops) des éléments est 16 si toutes les valeurs
sont différentes. Nombres positifs: balayage des nombres de la
matrice et bascule Pos mise à 0 dès la
rencontre d'une valeur négative (break). Vérification de la somme magique pour se
rassurer; inutile, car les formules assurent la magie. Si ses trois conditions sont réunies et, en plus,
si la somme vaut 88, impression de la matrice |
|
|
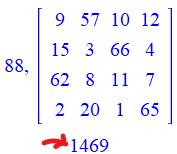
Quelques sorties parmi les 1469
carrés magiques possibles avec les contraintes
|
||
|
Valeur minimale de la somme
magique: 37 |
|
|
Voir Programmation – Index
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/CarreMag/CMor4Cas.htm
|
![]()