|
||||||||||||||||||||||||||||||||
![]()
|
Carré magique 4 x 4 Formules génériques Liens entre chaque case. Équations dans le carré magique. Attention: les
formules génériques fournissent des carrés magiques, mais pas forcément un
carré classique, avec les nombres qui se suivent de 4 à n². |
Donnez-moi les formules tout de suite: génériques, différentielles
|
|
|
|
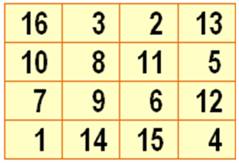
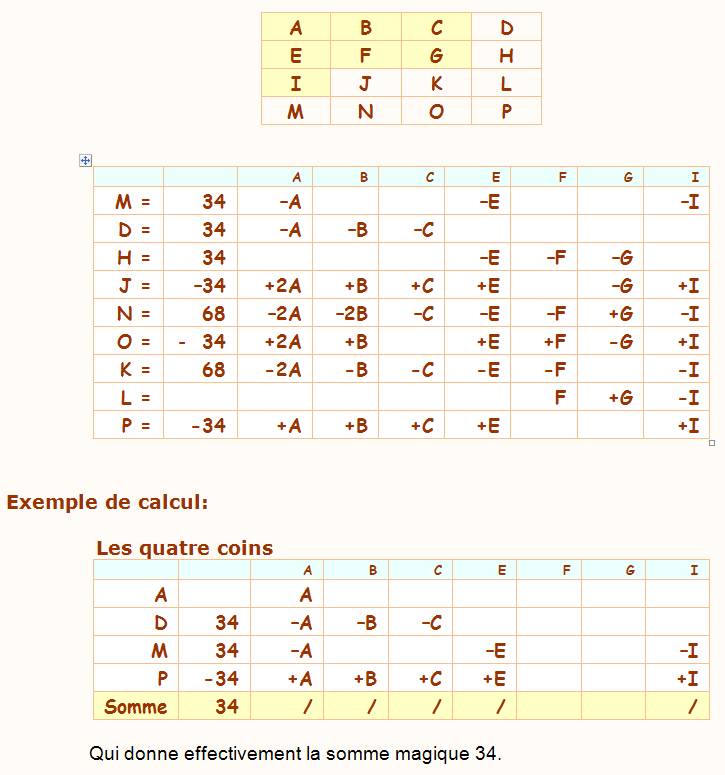
Sur cet
exemple de carré magique 4x4, avez-vous remarqué que la somme des cases
centrales est 34, la somme magique. Il existe
d'autres relations, faciles à montrer. Relations
Sommes
magiques Somme des quatre cases centrales = 34. Somme des quatre sommets = 34. Somme des cases médianes opposées = 34. En jaune la somme magique et en jaune
et marron les égalités dites égalités chapeaux)
|
|
|
|
|||||||||||||||||||
|
|
|
||||||||||||||||||
|
|
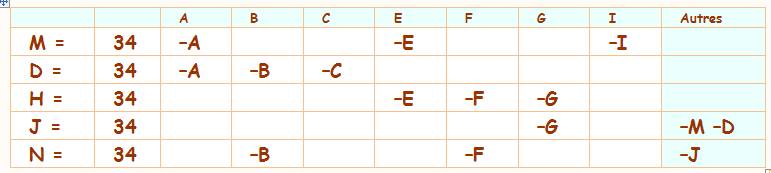
M = 34 – (A + E + I) D = 34 – (A + B + C) H = 34 – (E + F + G) |
|
|||||||||||||||||
|
|
J = 34 – (M + G + D) N = 34 – (B + F + J) |
|
|||||||||||||||||
|
La suite nécessite la
résolution d'un système d'équations. Ou la
connaissance a priori d'une propriété des carrés
magiques: L + I = F + G Nous allons
développer la résolution du système d'équations; un très bon exercice! Le calcul est
assez simple, mais nécessite beaucoup de soins. |
|||||||||||||||||||
|
|
|
|
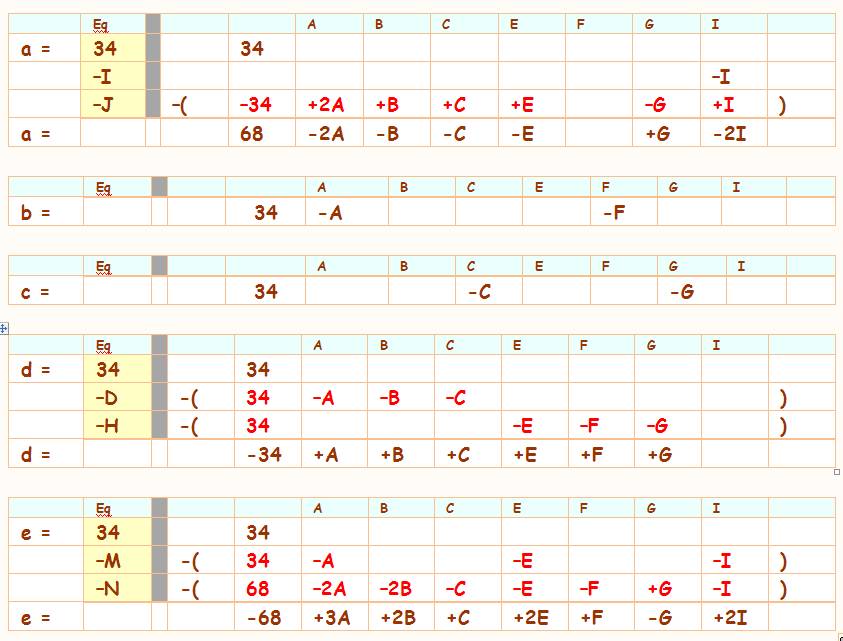
Ce
que nous savons en fonction des variables
indépendantes (A, B, C, E, F, G, I)
Calcul
de J et N en
fonction des variables indépendantes
|
|
|
|
|
|
On cherche à exprimer les quatre
cases blanches inconnues: Sommes
horizontales, verticales et la diagonale.
|
|
|
Calcul des variables
intermédiaires |
|
|
Nous connaissons nos quatre inconnues, mais avec les
variables intermédiaires a, b, c, d et e. Nous allons développer leur valeur
en fonction des variables indépendantes.
|
|
|
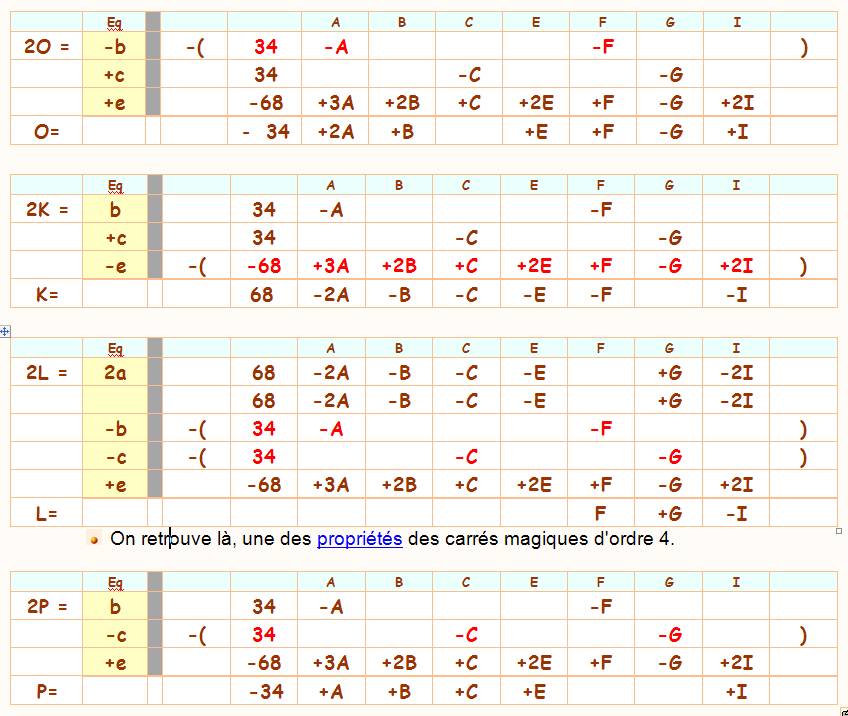
Développement final |
|
|
|
|
|
|
|||||||||||||||||
|
Formules
de Berholt ou différentielles
(élégance de la symétrie) Variables indépendantes: A, B, C, D, a, b, c et d.
Outre les lignes, colonnes et diagonales, on trouve
d'autres configurations magiques:
Propriété des carrés
magiques 4 x 4:
Ex: (A – a) + (B + b) = (A – a + d) + (B + b – d)
Ex: (B) + (C) = (C - b + d) + (B + b - d)
|
|||||||||||||||||
Voir Application au cas d'une date anniversaire incluse dans
le carré
|
|
|||||||||||||||||
|
Variables indépendantes : A, B, C et D
Somme magique: 34 Toujours les mêmes propriétés. En plus, les pandiagonales sont magiques: Ex: (B + D – A) + (17 - C) + (17 + A - B - D) + (C)
= 34 |
|||||||||||||||||
|
|
|||||||||||||||||
|
Seules les lignes et colonnes forment la
somme magique, pas les diagonales. Variables indépendantes : de A à I
|
|||||||||||||||||
![]()
|
Suite |
|
|
Voir |
|
|
Diconombre |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/CarreMag/CMor4Gen.htm |
![]()