NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 30/09/2011 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	Ésotérisme
Débutants Général	PYRAMIDES	Glossaire Général
INDEX Ésotérisme Histoire	Sommaire de cette page >>> Le secret des pyramides >>> Pyramide de Kheops >>> Rectangle d'or >>> Délires pyramidaux >>> Calcul de Napoléon >>> Construction

Pyramides (2500 av. J.-C.)

Pharaon Kheops (2538-2516 av. J.-C.): il fit construire la Grande Pyramide de Gizeh (pyramide de Kheops) qui abrite sa dépouille.

L'une des sept merveilles du monde antique.

Pharaon Khephren (vers 2500 av. J. -C.), successeur de Kheops, il fit construire la deuxième pyramide de Gizeh.

Pharaon Mykerinus: constructeur de la 3^e pyramide de Giseh.

Gizeh ou Guizèh, ville sur la rive gauche du Nil, on y trouve les trois pyramides et le Sphinx.

Les quelques citations et données suivantes sont principalement extraites du livre "Le secret de la Grande Pyramide" de Georges Barbarin.

LE SECRET de la GRANDE PYRAMIDE

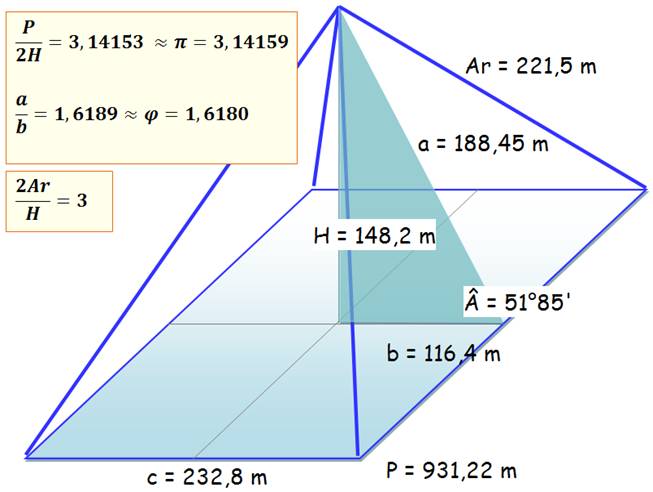
Dimensions Quelques mesures principales de la Pyramide, en chiffres de notre système métrique. Les mesures de l'astronome Piazzi Smith correspondent à : Base carrée de côté 232, 805 mètres Hauteur 148, 208 mètres Quantité de pierres 6 millions Quantité de couches 200 Le circuit de base de la Pyramide est de 36 524 pouces, nombre qui correspond cent foi le nombre de jours de l'année. Les diagonales de la base font 25 826,5 pouces et la hauteur totale est de 5 813 pouces (axe vertical central). Orientation Aves les premiers astronomes et premiers géomètres du monde, l'orientation de la Grande Pyramide vers les quatre points cardinaux est irréprochable: elle est exacte, à quatre minutes trente-cinq secondes près (autre source: 3'6). Le couloir descendant est aligné avec l'étoile polaire. Pi et la quadrature du cercle Aujourd'hui on peut calculer la valeur de Pi avec n'importe quel nombre de décimales, sans jamais trouver la dernière, ce qui démontrerait que la quadrature du cercle est une définitive impossibilité. Avant Jésus-Christ les données oscillaient entre 3 10/70 et 3 10/71. Du temps des Pharaons, avait-on une valeur très précise de Pi? Divisons le périmètre de la Pyramide (931,22 m) par deux fois l'axe vertical (148, 208 m x 2): 931,22 / (2 x 148,208) = 3,141598 … À comparer à Pi = 3,141592654 … Rayon de la Terre Constatation du célèbre directeur de l'Observatoire de Bourges: la coudée sacrée, soit 0,635 660 m, multipliée par dix millions, égale 6 356 600 mètres, rayon polaire de la Terre (6 356,8 km). Distance Terre-Soleil – Historique Dates Évaluation Valeur en km

Voir Distance Terre-Soleil / Histoire / Savants / Histoire des sciences

PYRAMIDE de KHEOPS – Dimensions
Périmètre de la base 931,22 m Côté du carré de la base 232,8 m Hauteur 148,208 m Aire de la base 54 196 m² = 5,4 hectares (c²) Aire latérale 21 936 m² (ac/2) Volume 2,68 10^6 m^3 (H.Ab /3) Périmètre du cercle R=H 931,22 m égal au périmètre de la base

Voir Nombre Pi / Nombre d'or / Nombre 147

RECTANGLE d'OR

Les faces de la pyramide sont formées des deux moitiés d'un rectangle d'or. Autres explications Hérodote a écrit que la pyramide a été construite de sorte que la surface de chaque face est égale à la surface d'un carré qui aurait comme côté la hauteur de la pyramide. Aujourd'hui, aucun scientifique ne soutient la thèse de l'introduction volontaire de Pi et du nombre d'or (Phi) dans la construction de la pyramide. Il s'agit d'un hasard lié aux propriétés géométriques des angles choisis pour de simples raisons pratiques.

DÉLIRES PYRAMIDAUX

Seuls les extraterrestres ont pu aider les Égyptiens à construire les pyramides. Les paysans du Nil maîtrisaient la puissance des ultrasons et des forces antigravitationnelles. Les pyramides sont les jalons d'un méridien mondial ou la capsule temporelle renfermant le savoir d'une culture oubliée. Un modèle de l'arche de Noé. Un observatoire astronomique. Une centrale nucléaire (!?) La chambre du Roi permet d'aiguiser les pouvoirs psychiques en vue de pratiquer la désintégration mentale. Etc.

CALCUL DE NAPOLÉON

"La pyramide pourrait fournir les matériaux d'un mur haut de six pied, qui aurait mille lieues et ferait le tour de la France".

On ne sait pas si c'est Fourier ou Napoléon qui aurait fait ce calcul.

Construction d'un mur avec les pierres de la pyramide

Pyramide	Volume	148,2	x 233²	/ 3 =	2 681 800	m^3
Mur	Largueur	0,30				m
	Hauteur	3				m
	Longueur	2 681 800	/ (3	x 0,3) =	2 979 000	m
France	Superficie	551 695				km²
	Côté carré	742 760				m
	Périmètre	742 600	x 4	=	2 970 400	m
En fait:	Frontières	(terre,	mer	et...Corse)	5 663 000	m

 Voir Frontières de la France

La méthode utilisée par Napoléon, considérant la France comme un carré, donne un mur de 3 m de haut sur toute la France. Mais, les frontières sont tourmentées. Avec les pierres de la pyramide, dans les mêmes conditions, on ferait un mur de 1,5 m de haut et non pas les 3 mètres comme l'avait calculé Napoléon.
Notez que la superficie de le France devrait tenir compte du fait que du temps de Napoléon la Belgique était en France.

CONSTRUCTION

Comment les Égyptiens ont-ils transporté les énormes blocs de pierre au sommet de la pyramide? Hypothèse: les blocs de pierre sont glissés sur des traineaux le long d'une rampe qui suit le contour de la pyramide à sa périphérie, formant une sorte de spirale carrée. La rampe serait composée d'une succession de 21 galeries, parallèles aux faces de la pyramide. Dans les années 2000, l'architecte Jean-Pierre Houdin travaille sur cette hypothèse et apporte une confirmation. Il interprète la présence de pièces particulières aux angles de la pyramide comme la zone de manutention des blocs, opération destinée à placer ces blocs en position pour poursuivre leur ascension sur la volée de la face suivante. Les pièces d'angles seraient donc des paliers permettant le changement de direction (une rotation de 90°) des traineaux. La manutention est effectuée à l'aide de grues rudimentaires, sans doute préfigurant les chadoufs égyptiens permettant de puiser l'eau dans les puits. Pour être plus précis, cette technique serait celle utilisée dans la partie haute de la pyramide. Les galeries étant installées à une bonne dizaine de mètres à l'intérieur de la pyramide. Pour la partie basse, une rampe externe faisait l'affaire. Elle permettait de monter jusqu'à 43 mètres et d'effectuer 64% de la construction. Volume pyramide supérieure / Volume pyramide totale = (148,2-43)^3 / 148,2^3 = 0,357 = 35,7%; soit 100 – 35,7 = 64,3% pour la partie basse). Attaquant la partie supérieure, la rampe externe était démontée et servait de réservoir à blocs de pierre pour construire la partie supérieure.

Source: littérature scientifique de janvier 2011 dont Sciences et Avenir

Suite	Nombre pyramide Pyramide (polyèdre) Pyramide des âges Ésotérisme – Index Labyrinthes
Voir	Cabale Gémâtrie Millenium Numérologie Pythagore