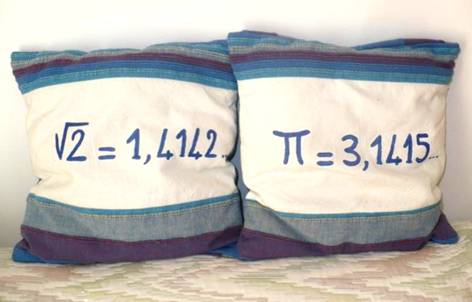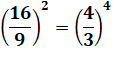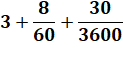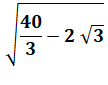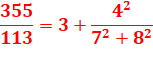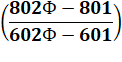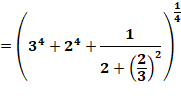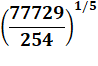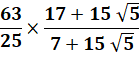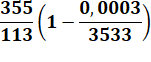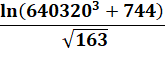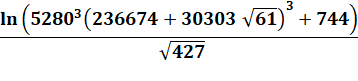NOMBRES – Curiosités, Théorie et Usages

 

Accueil                           DicoNombre            Rubriques           Nouveautés      Édition du: 19/03/2024

Orientation générale        DicoMot Math          Atlas                   Actualités                       M'écrire

Barre de recherche          DicoCulture              Index alphabétique        Références      Brèves de Maths

             

Constante

 

Débutants

Constante PI

Généralités

 

Glossaire

PI

 

 

INDEX

 

Constante PI

 

Introduction

Calcul

Formules

Propriétés

Historique

Valeur

Décimales

Curiosités

Valeur (Suite)

Programmation

 

Sommaire de cette page

>>> Valeurs

 

 

 

Curiosité

Amusement: nombres coussins

P1030981

 

Deux constantes remarquables, qui nous offrent des analogies:

*        Coïncidence de 1414 et 1415.

*        Chacune est composée d'une succession de deux chiffres 41/42 et 14/15;

*        Elles n'utilisent que les chiffres de 1 à 5;

 

Voir Racine de 2

 

VALEUR DE

 

Cent premières décimales de Pi

 

 

Voir Mnémotechnique

Trois Glorieuses

3, 14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944

59230 78164 06286 20899 86280 34825

34211 70679

                … >>>

 

Bonne approximation

 

Construction

 

Voir Réduites de Pi

 

  355 / 113 = 3,141 592 9

 

Nombres impairs doublés : 11 33 55

Les trois derniers divisés par les trois premiers: 355 / 113.

La somme de ses 145 premières décimales de Pi est égale à 666, ce qui en fait un nombre du diable.

Anglais: Pi value to 100 decimal places

 

Expression habituelle pour la valeur de Pi

Pourquoi dit-on: Pi égal trois, quatorze cent seize?

*    D'abord il s'agit d'une approximation (légitime):  

*    Ensuite, un usage (ancien) veut que les premiers milliers se disent indifféremment: mille-quatre-cent-seize ou quatorze cents seize.

*    Enfin, pour cette phrase mnémonique, on omet de nommer la virgule tout en la marquant par un temps d'arrêt à l'oral.

 

Il est préférable de dire: Pi égal trois virgule mille-quatre-cent-seize ou d'énoncer les décimales une à une ou par blocs de deux: Pi égal trois virgule quatorze, quinze, quatre-vingt-douze, etc.

Charade

Mon premier: bièvre qui travaille debout;

Mon deuxième: bièvre qui travaille debout;

Mon troisième: bièvre qui travaille debout;

Mon tout: une constante mathématique bien connue.

Réponse: trois castors sans chaise.

Bièvre, ancien nom du castor; encore connu par le nom de localités comme la vallée de la Bièvre (Guyancourt – Yvelines).

Voir Écrire les nombres en lettres / Jeux de mots

 

 

Définition de mots croisés: chiffre rond.

Réponse : PI

Rond fait référence au cercle dont Pi est une constante.

Voir Mots croisés / Humour

 

 

 

VALEURS

 

VALEURS COMPARÉES DE  

par ses APPROXIMATIONS rationnelles et algébriques

 

Nd = Nombre de décimales justes (soit 1 de plus, avec le 3, pour tous les chiffres significatifs) 

 

 

Ndéc

Approximation

Valeur

Écart

Pi – Approx

An

Qui

0

 

3

1,4

10-1

 

Bible

0

2  

3,2

-9

10-2

 

Nombre d'or

1

 

3,1

4

10-2

100

Chine

1

3,162

-2

10-2

600 

Inde

Racine de 10

1

3,160

-1,9

10-2

-1 650

Égypte

Papyrus Rhind

1

3,125

1,6

10-2

- 2000

Babyloniens

1

142 / 45

3,155

-1,4

10-2

250

Chine

 

2

3,1464

-4,8

10-3

1968

2

3,1462

-4,7

103

 

 

2

3,1446

-3,0

10-3

 

 Voir

 Rectangle de Kepler

2

Pour référence

3,14

1,6

10-3

 

 

2

3,1428

-1,3

10-3

 

 Réduites de Pi

2

104 384 / 33 215

3,142

-1,0

10-3

 

3

 Pour référence

3,141

5,9

10-4

 

 

3

3,1421

-5,6

10-4

A. Povolotsky

3

3,1411

4,9

10-4

3

3,1411

4,2

10-4

3

3,14185

-2,6

10-4

-250

Archimède

3

864 / 275

3,1418

-2,3

10-4

1 220

Fibonacci

3

311/3

3,14138

2,1

10-4

3

1,9

10-4

530

Inde  >>>

3

3,141428

1,6

10-4

3

3,14172

-1,2

10-4

 

Castellanos

3

3,1417

3,1417

-1,1

10-4

-100

Ptolémée

 

4

Pour référence

3,1415

9,2

10-5

4

333 / 106

3,141509

8,3

10-5

3

3,14167

-7,4

10-5

-100

Ptolémée

3

3.14165

6,4

10-5

2020

 J.-L. Breuil

Voir Construction

4

3,14153

6,3

10-5

1988

 Castellanos

3

3,14165

6,3

10-5

Voir approximations avec les nombres de Fibonacci

4

3,14153 3

5,9

10-5

 Kochansky

4

437/23

3,14153 9

5,3

10-5

3

3,14164

-4,8

10-5

4

3061/5

3,14155 2

4,0

10-5

3

3,14164

-4,8

10-5

1600

Hobbes, Ramanujan

3

211 875 / 67 441

3,14163

-4,2

10-5

-250

Archimède

3

3,14163

3,9

10-5

2008

Schneider

4

3,14156

2,5

10-5

3

3,1416

-7,3

10-6

263

Chine (Liu Hui)

3

62 832 / 20 000

3,1416

-7,3

10-6

530

Inde

 

 

6

 Pour référence

3,14159 2

6,5

10-7

6

3,14159 29

-2,7

10-7

450

Chine: Tsu Chung Chih

Fraction Pi

 

Construction de ce nombre

6

3,14159 24

2,0

10-7

Castellanos

6

3,14159 255

1,01

10-7

6

1,09999901 x 1,19999911 x

1,39999931 x 1,69999961

3,14159 25

8,1

10-8

 

Formule célèbre de Ramanujan

Dans son cahier de notes de 1910, Ramanujan avait écrit 17 façons de développer 1/Pi en série. La suivante est restée célèbre. Elle produit huit décimales à chaque itération. Elle a été utilisée en 1985 pour calculer 17 millions de décimales.

Le premier terme donne déjà une excellente approximation.

C'est seulement en 1987 que cette formule a été démontrée par les frères Jonathan et Peter Borwein.

Cette formule est basée sur cette coïncidence numérique:

Voir Nombre 104 / Nombre 163

 

 

 

6

3,14159 273

-7,6

10-8

Ramanujan

7

3,14159 2639

1,4

10-8

K. Rashid

7

3,14159 2649

5

10-9

Fractions égyptiennes

7

3,14159 264

7,8

10-9

Fractions unitaires

8

3,14159 26525

1,0

10-9

Ramanujan

8

3,14159 26526

1,0

10-9

Ramanujan

 

9

Pour référence

3,14159 2653

5,9

10-10

9

103 993 / 33 102

3,14159 26530 1

-5,8

10-10

Euler

8

3,14159 2654

-5,2

10-10

Castellanos

9

3,14159 26538

-2,1

10-10

Ramanujan

9

208 341 / 66 317

3,14159 26534

1,2

10-10

 

10

Pour référence

3,14159 26535

8,9

10-11

1 579

Viète

9

312 689 / 99 532

3,14159 26536

-2,9

10-11

14

3,14159 26535 89794

-1,1

10-15

Ramanujan

15

Pour référence

3,14159 26535 89793

2,4

10-16

 

 

30

3,14159 26535 89793 23846 26433 83279 7

-2,2

10-31

Utilisation d'un

Nombre de Heegner

51

 

Valeur de Pi avec 31 décimales (pour comparaison)

 

 

 

 

 

Suite

*  Valeurs approchées de Pi – Suite 

Codage de Pi en base 2 et en virgule flottante

Décimales de Pi et jeux

Formule impliquant Pi – Exemples

Formule pannumérique de Plouffe  et Ed Pegg Jr, indépendamment

Nièmes chiffres de PI

Pi avec Pi, Phi et e

Pi et nombres de Fibonacci

Pi pannumérique

Point de Feynman: Pi un nombre presque entier?

Puissances de Pi

Valeurs de Srinivasa Ramanujan (le "Euler" Indien)

Suite sur PI

*  Table des décimales de Pi

*  Décimales de Pi – Course aux décimales

*  Historique du calcul de Pi

*  Mnémotechnique de Pi

*  Quadrature du cercle et approximation de Pi

*  Réduites de Pi – Calculs

*  Approximations de Pi par des racines

*  Approximations de Pi avec la suite de Farey

Voir

*  Arc tangente

*  Calcul mental – Index

*  Cercle

*  Constantes Mathématiques

*  Fraction – Glossaire

*  Géométrie – Index

*  Pi – Glossaire

*  Quadrature du cercle

*  Rubick's cube

*  Théorie des nombres – Index

DicoNombre

*  Nombre 3,14

Livre

*   Le fascinant nombre Pi – Jean-Paul Delahaye – Belin – Ed2 de 2018

Site

*   Approximations de Pi – Wikipédia

*   Pi Approximations – Wolfram MathWorld

Cette page

http://villemin.gerard.free.fr/Wwwgvmm/Geometri/PiValeur.htm