|
||||||||||||||||||||||||||||||
|
Voilà
les résultats José. La bonne nouvelle c'est que l'ordinateur a bien passé le test de Turing. La mauvaise, c'est que toi, par
contre, tu l'as raté! Les
machines un jour pourront résoudre tous les problèmes, mais jamais aucune
d'entre elles ne pourra en poser un ! Einstein Les
gens normaux... croient que si ça marche, c'est qu'il n'y a rien à réparer.
Les ingénieurs croient que si ça marche, c'est que ça ne fait pas encore assez de choses. Scott Adams, Le principe de Dilbert |
Voir Pensées & humour
|
ALAN TURING & MACHINE DE
TURING Alan Turing (1912-1954): le "ADAM"
des ordinateurs. Tous les ordinateurs et
microprocesseurs d'aujourd'hui sont encore basés sur le principe énoncé par
Turing. Son aspect élémentaire et
basique sert également à déterminer si un calcul peut être réalisé sous forme
automatique (algorithme). |
Anglais : Turing
machine
|
Nous (Parenthèse Cinéma) souhaitons vous informer
de la sortie au cinéma le 28 janvier 2015 du film IMITATION GAME, réalisé par
Morten Tyldum. Graham
Moore (né en 1981) a reçu l'Oscar du meilleur scénario adapté en février
2015. Il s'agit de l'adaptation de la biographie: Alan Turing ou l'énigme de
l'intelligence (Alan Turing: The Enigma) d'Andrew Hodges (1992). 1940 : Alan Turing,
mathématicien, cryptologue,
est chargé par le gouvernement britannique de percer le secret de la célèbre
machine de cryptage allemande Enigma, réputée
inviolable. À la tête d’une équipe improbable de savants, linguistes,
champions d’échecs et agents du renseignement, Turing s’attaque au
chef-d’œuvre de complexité dont la clef peut conduire à la victoire. C’est le
portrait d’un homme qui contribua à changer le cours de la Seconde Guerre
mondiale mais se retrouva condamné par la société de l’époque en raison de
son homosexualité et en mourut. Nous avons rédigé un dossier pédagogique
destiné plus particulièrement aux professeurs d’histoire et de mathématiques.
Il comprend de nombreux éclairages sur la vie et les travaux d’Alan Turing,
le fonctionnement de la machine Enigma et le
contexte historique. Ce dossier propose également plusieurs décryptages à
résoudre en classe, avec à la clé des places de cinéma à gagner pour
découvrir le film. Vous pourrez le télécharger sur le site du film à la
rubrique « Document pédagogique » en cliquant ICI |
Biographie d'Alan Turing
|
|
||
|
Un génie à la scolarité laborieuse: son bulletin scolaire de 1929
déplore son niveau faible en lecture, un niveau médiocre en français et des
capacités formidables en mathématiques gâchées par un travail désordonné.
|
Au Cambridge King's
Collège.
Du temps de Bletchley
Park.
Marin au périscope d'un sous-marin.
Symbolise la réussite de Turing à décrypter l'Énigma
navale (baptisée Dolphin). |
|
|
Énigma |
La
B.O.M.B.E |
|
D'après RTS.Ch
25/12/2013 – & nombreux articles dans la Presse
Biographie
chronologique d'Alan Turing
|
1912 |
0 |
Naissance à
Londres |
|
1926-31 |
14 à 19 |
École de Sherborne. |
|
1930 |
18 |
Mort de son ami Christopher Morcom. |
|
1931-34 |
19-22 |
King's College (Université de Cambridge). |
|
1932 … |
20 |
Mécanique quantique, probabilité,
logique… |
|
1933 |
21 |
Il connait les travaux de Bertrand
Russel sur les fondements de es mathématiques. |
|
1936 |
24 |
Machine de Turing, calculabilité,
calculateur universel. Gödel
ne conclut pas sur la décidabilité en mathématiques. Turing va s'y attaquer. |
|
1936-38 |
24-26 |
Université de Princeton. Ph.D en
logique, algèbre, théorie des nombres. |
|
1936-37 |
/ |
Publie: On
computable numbers, with
an application to the Entscheidungsproblem, texte
qui se rapporte à la machine de Turing. |
|
1938-39 |
26-27 |
Retour à Cambridge. Traite de la machine Énigma. |
|
1839-42 |
27-30 |
Conçoit la "BOMBE", machine
de décryptage d'Énigma avec le mathématicien Gordon Welchman. |
|
1942 |
30 |
Décrypte les messages d'Énigma marine
installée à bord des sous-marins allemands. |
|
1943-45 |
31-33 |
Chef consultant en cryptologie auprès
des Américains. |
|
1945 |
33 |
National Physical
Laboratory à Londres. |
|
1946 |
34 |
Concepteur précurseur en calculateurs
et en programmation. Turing
conçoit les plans du premier ordinateur moderne, mais n'a pas les moyens de
le réaliser. |
|
1947-48 |
35-36 |
Programmation, réseaux de neurones,
intelligence artificielle. |
|
1948 |
36 |
Université de Manchester avec premières
applications mathématiques sur ordinateurs. Il anticipe de plusieurs décennies
l'intelligence artificielle et les réseaux de
neurones. |
|
1950 |
38 |
Test de Turing caractérisant
l'intelligence d'une machine. Il est le premier à écrire des programmes informatiques, dont le
programme d'un jeu d'échecs dont ses collègues
se moquent. Une passion inutile, disent-ils. |
|
1951 |
39 |
Fellow of the Royal Society (FRS). Théorie non-linéaire de la vie
biologique |
|
1952 |
40 |
Arrêté pour homosexualité. Perd ses habilitations en matière de
sécurité. |
|
1953-54 |
41-42 |
Travaux sur la biologie et la
physique restés inachevés. |
|
1954 |
42 |
Décès par empoisonnement au cyanure:
meurtre ou empoisonnement? |
Sportif
|
Marathon en 2 h 46 min
3 s. Seulement 11 s de plus
que le champion olympique de l'époque (1948). |
Décryptage de la machine Énigma
|
|
||
|
Principe du codage Énigma
Une lettre à coder est transformée par trois rotors
puis une boite de câblage pour ressortir sous une forme cryptée. à travers
ces arcanes la lettre A, par exemple, devient K.
(5 x 4 x 3) x (263) = 1 054 560 possibilités.
26! / (6! x 10! x 210) = 150 738 274 937 250 possibilités.
158 962 555 217 826 360 000 possibilités. |
Machine
Énigma
|
|
|
159 1018 / (106 x 3600 x 24 x 365,25) = 5 000 000 années.
|
…
et la "bombe" de Turing pour décrypter Énigma (celle-ci fut construite par l'US Navy avec l'aide de Turing)
Grâce à l’ingéniosité de Turing et de ses collègues, la plupart des
messages allemands interceptés sont
décryptés dès 1942. Les Polonais avaient développé leurs propres méthodes adaptées au
premières versions d'énigma. Turing contribue à la construction des
"bombes" plus sophistiquées utilisées par la Marine allemande,
notamment à bord des sous-marins
(U-Boat). |
|
|
Turing
cherche à décoder les machines de cryptage comme
un scientifique essaie de trouver les lois de la nature. |
|
Turing, un homme décisif pour la victoire
de 1945 En 1939, de
retour de Princeton, Turing est convoqué à Bletchley
Park avec un autre mathématicien et des personnes d'horizons divers. Le but;
décoder les messages radio des Allemands. l'équipe dispose d'une machine
Énigma venue de Pologne sans en connaitre le mode d'emploi. Les Allemands
considèrent leur machine Énigma comme la machine de cryptage absolue. Turing à l'idée
d'une machine pour casser le codage: le BOMBE. Elle sera fabriquée en série
et va décoder des milliers de messages. C'est la première fois que la machine
empiète sur l'intelligence
humaine; le début de l'intelligence artificielle. Les combats
aériens sont désormais en faveur des Britanniques. Les Allemands se reportent
sur la guerre sous-marine. Établissement de la base des sous-marins à Lorient. L'amiral
Dönitz met en place la tactique de la meute: un SM
en patrouille qui détecte un convoi américain en informe le QG, lequel focalise tous les SM sur le convoi. C'est
20 navires qui coulent d'un coup! La machine
Énigma des U-boat, baptisée Dolphin, est plus
complexe que la machine terrestre. La Hut 8 à Bletchley est dédiée à la machine Dolphin,
à sa tête Alan Turing. Après des semaines de recherches, Turing a la
révélation en une nuit: utiliser les statistiques, traquer les
"résonances" (coïncidences) et pondérer les possibilités. Sa
méthode est nommée Banburisme. L'équipe reçoit
un coup de pouce du fait de la saisie d'une machine Énigma, avec ses codes
pour quelques semaines, dans un SM en difficulté, abandonné par les Allemands
et investi par les Britanniques. Tous les messages allemands sont décodés et
les convois protégés des attaques des U-Boat. Turing et trois
collègues plaident en faveur de moyens auprès de Churchill qui les leur
accorde. Bletchley passe de l'artisanat à une
véritable industrie. Fin 1941, les
États-Unis entrent en guerre. Les Allemands
inventent une nouvelle machine de cryptage (Tunny) basée
sur le code numérique des télescripteurs et non plus le morse. Turing en réalise une réplique
assez rapidement, et finit par décoder les messages. Cette fois, ce sont les
Russes qui vont profiter des informations interceptées. Ils repoussent une attaque fomentée par
Hitler et se dirigent vers Berlin. Le décodage des
messages reste laborieux. Turing cherche à le systématiser avec une
machine. Tommy Flowers
(1905-1998) est spécialiste des tubes à vide et se propose de réaliser cette
machine qui comporterait de l'ordre de 2000 lampes. Sur un critère de
fiabilité, son projet est refusé. Têtu, il se lance malgré tout dans le
projet. Il développe Colossus, le premier
ordinateur électronique programmable du monde, et va aider à décrypter les
messages allemands. Le rêve de Turing est réalisé. |
Colossus En 1944, Colossus
décode tous les messages allemands et va servir à tester la réception d'une
grande manœuvre d'intoxication. Il faut faire
croire aux Allemands que le débarquement aura lieu à Calais (opération
Fortitude). Ce qui sera le cas. |
|
À la fin de la guerre,
Turing et ses collègues sont laissés dans l'ombre, secret militaire oblige.
Même, Turing en sait trop, il est une menace pour le gouvernement
britannique. 1945 – Turing
conçoit les plans du premier ordinateur moderne, mais n'a pas les moyens de
le réaliser. 1948 – Il
anticipe de plusieurs décennies l'intelligence artificielle et les réseaux de
neurones. 1950 – Il est le
premier à écrire des programmes
informatiques, dont le programme d'un jeu
d'échecs dont ses collègues se moquent. Une passion inutile, disent-ils. |
Turing continue
son entrainement à la course à pied et passe très près de la sélection pour
les Jeux Olympiques. Il a une aventure avec un jeune homme et, en mars 1952, il
est condamné pour outrage aux mœurs. Pour vaincre son homosexualité, il devra
subir une castration chimique. Son corps change. Il est inquiet. Il a du mal
à se concentrer … On le retrouve mort en juin 1954 avec du cyanure dans le
corps et une pomme sur sa table de nuit. En 2013, la
reine accordera son pardon royal. |
Voir Histoire
des ordinateurs / Histoire de
l'informatique
Machine théorique de Turing
|
|
|
|
Chaque
fois qu'il y a une suite de 1 (Chaîne de 1). Je
souhaite ajouter un et un seul 1 à la suite. Départ 0
0 1 1 1
0 0 Arrivée 0
0 1 1 1
1 0 Principe
en
séquence de la gauche vers la droite, et former
une autre chaîne en fonction des données de chaîne de départ.
Il
utilise une bande perforée qui défile devant la tête d'un lecteur, la
chaîne de bits ayant été inscrite sur la bande. La
nouvelle chaîne de bits sera imprimée sur une
autre bande. Je vais simplifier
la machine historique de Turing pour les besoins d'une introduction simple. |
|
|
|
|||||||||||
|
Ce
que l'on cherche L'idée consiste à recenser les ordres qui sont communs:
chaque fois que c'est comme ça, je fais cela. Le but étant de disposer d'ordres (instructions) très généraux. Tentative On pourrait dire chaque fois que:
Mais, on a constaté que ce n'est pas toujours vrai. Il faut tenir compte de l'état d'une variable (mémoire)
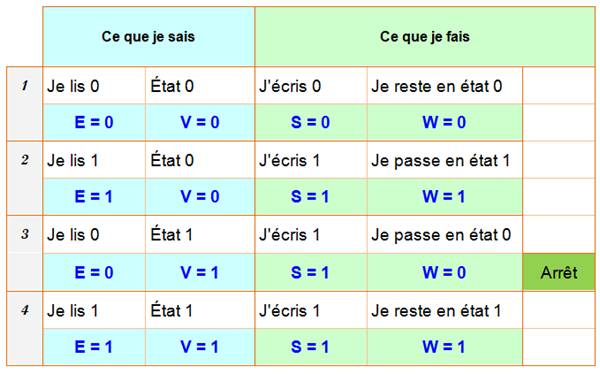
interne. On va donc trouver quatre cas possibles: Baptêmes
Quatre
cas possibles (Attention: récapitulatif logique et non chronologique)
|
|||||||||||
|
|
|
|
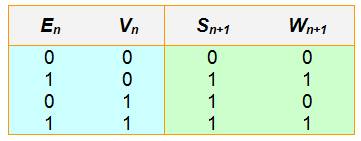
pour
chacun des bits, on
examine la liste des quatre instructions ainsi résumées:
|
|
|
|
|
|
Voir le
développement en automate |
|
|
|
|
|
Elle est expliquée dans le livre The emperor's New Mind de Roger
Penrose. |
|
Voir Théorie décidabilité / Toute pensée
est un (lambda) calcul
|
Jeu
qui consiste à isoler trois personnes: un homme, une femme et une tierce
personne. Celle-ci doit deviner qui est l'homme et qui est la femme, sachant
que "homme et femme" doivent s'employer à brouiller les cartes. Le
moyen de communication doit être neutre (dialogue via des ordinateurs par
exemple). Turing
s'inspire de ce jeu pour proposer son test – le test
de Turing – la tierce personne doit reconnaitre un humain ou un
ordinateur. En cas d'échec, la machine est réputée avoir réussi le test. Elle
a un comportement "humain". ELIZA, programme de conversation pionnier en
1964, puis ALICE, nettement plus performant en 1995 sont les plus connus des agents conversationnels (chatbot
ou chatterbot). Sans réussir le
test de Turing, ALICE a remporté le prix Loebner
relatif au test de Turing. Vous
pouvez vous amuser avec ALICE sur
Internet:
|
|
Suite |
|
|
Voir |
|
|
Livre |
|
|
Sites |
|
|
Film |
|
|
Cette
page |
