|
||||||||||||||||||||||||||||||||||||||||
![]()
|
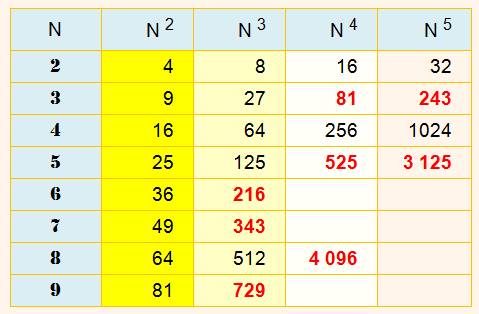
Puissances de 2 à 5 des nombres de 2 à 9 Tables et
apprentissage. |
|
|
||
|
|
4, 9, 16, 25, 36, 49, 64, 81 2, 4, 8,
16, 32, 64 … 4, 16, 64,
256 8, 64, 512 5, 25, 125 |
|
|
|
|
|
On complète par quelques puissances de 2 et multiples.
Remplissage:
18/32 = 56 % |
|
|
|
||
|
On se souviendra de la règle générale pour les nombres multiples de
3, la somme des chiffres doit être un multiple de trois. Et multiple de 9 pour les puissances du
nombre 9. |
63
= 216 6
x 6 = 36 et x 6 = 216 73
= 343 Cube
palindrome en 3 aux extrémités. 93
= 729 La
somme des chiffres doit être égale à 9. Ici, en plus du 9 existant, c'est
fait avec 7 + 2 |
|
|
|
34
= 3² x 3² = 9 x 9 = 81 35
= 81 x 3 = 243 54
= 125 x 5 = 625 = 25 x 25 55
= 625 x 5 = 3 125 Se
termine par 25 et 6 x5 = 30 plus une retenue donne 31 |
|
|
Remplissage: 25/32 = 78 % |
||
|
|
||
|
|
65
= 7 776 Configuration
typique mémorisable Quant
aux autres, pas facile … |
|
|
|
||
|
|
|
|
Exemple les nombres de rang 6, 15, 21 et 26
utilisent une puissance de 5 Rappel, il s'agit uniquement des puissances
2 à 5 des nombres de 2 à 9 |
|
Formules de passage entre les puissances

![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()