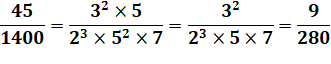|
||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
NOMBRES DÉCIMAUX
Tous les nombres de ce tableau sont
des nombres décimaux.
Attention: le mot décimal est très employé! >>> Attention: tous les nombres à virgule ne sont pas décimaux. Définition: Nous
comptons avec des nombres
entiers qui s'écrivent selon une forme
décimale (base 10). Certains
nombres comme les nombres
rationnels (fractions)
s'écrivent aussi sous forme décimale: ils sont constitués d'une partie
entière et d'une partie décimale, séparés par une virgule. On dit que ces
nombres à virgule sont des nombres décimaux. |
|
|
||
|
Un achat en euros peut comporter des
centimes. Une longueur se mesure en mètres,
centimètres … Voir Déci,
centi, milli … Certaines
divisions s'arrêtent (reste nul): |
Dans tous ces cas, on
emploie alors les nombres à virgule, la
quantité de chiffres après la virgule étant limitée. Ce n'est pas le cas
avec un nombre tel que Pi qui vaut
3,141592 … avec des chiffres sans fin. Ce n'est pas le cas de
1/7 = 0,142857 142857 … avec des chiffres sans fin, même si ce sont les mêmes
qui se répètent. Les nombres avec
virgule et quantité limitée de chiffres sont des nombres
décimaux. Les nombres entiers (sans virgule ou avec une virgule suivie de
0) font partie de cette famille. |
|
|
|
||
|
Système décimal Nous comptons ave le système
décimal, c'est-à-dire avec des puissances
de 10, aussi nommé système de numération
de position. Les chiffres présents dans le nombre sont les chiffres significatifs; les derrière la virgule sont les décimales.
Soit le nombre négatif = – 13,45 =
– 14 + 0,55
|
Exemple de nombre
décimal Avec interprétation de chacun des chiffres selon sa
position dans le nombre.
|
|
|
Développement décimal Lorsqu'un nombre rationnel (une fraction) est exprimé avec un nombre
à virgule, il s'agit de son développement décimal. Remarques sur les
fractions On peut développer toutes les fractions en un nombre à virgule,
mais toutes ne sont pas la représentation de nombres décimaux. Les nombres irrationnels
(non fractions) ont un développement décimal sans fin, composé de chiffres
toujours différents. |
Développement décimal
d'un nombre (Ne pas confondre avec "nombres
décimaux")
Voir
Développement
décimal / Développements
sur les nombres décimaux / Décimal
dans DicoMot Math |
|
Anglais pour séparateur décimal:
decimal point or radix point
Amusement
|
La
racine cinquième de 109 vaut 2, 555555
397. Avec six décimales à 5. |
Voir
Curiosité de formes avec les nombres
|
|
||
|
avec n entier
rationnel et m, a et b entiers naturels. Aussi Nombre
décimal:
Nombre fractionnaire à développement fini.
|
Place des nombres
décimaux
Voir Inventaires des
nombres / Nombres
périodiques |
|
|
|
||
|
Propriétés classiques Tout nombre décimal est un nombre rationnel. Un nombre décimal est la somme de sa partie entière et de sa partie
décimale. Exemple: 12,5 = 12 + 0,5 Il peut s'écrire comme la somme d'un entier et d'une fraction. La somme de deux nombres non-décimaux peut très bien être décimale. Entre deux nombres décimaux, il existe une infinité de nombres
décimaux. |
Propriétés avancées Les nombres décimaux peuvent s'écrire en utilisant un entier suivi
d'une puissance
négative. Tout nombre rationnel inférieur à 1 peut être représenté par une somme
de fractions égyptiennes. Les nombres décimaux forment un ensemble stable par l’addition et la
multiplication. L'ensemble est stable par la soustraction à condition
d'introduire les décimaux négatifs. L'ensemble n'est pas stable par la
division. L'opposé –n de n est un nombre décimal. L'inverse 1/n de n (non nul) n'est pas toujours un nombre
décimal. |
|
|
n
= 6/100 + 15/10 = 0,06 + 1,5 = 1,56
Division de 493 par 4
qui donne 123 comme quotient et 1 pour reste. Réponse: 1479 / 12 =
123 + 1/4
On peut aussi écrire directement: 75,05 =
7505/ 100 |
|
|
||
|
Une fraction représente un nombre
décimal si la fraction
irréductible qui lui est égale a un dénominateur qui peut être décomposé
sous forme d'un produit de puissances
de 2 et de puissances
de 5. Pour reconnaitre si une fraction
représente un nombre décimal, on peut:
|
Ces deux nombresci-dessus sont décimaux.
Ce nombre n'est pas décimal 9/280 = 0,032 142857 142857… |
|
|
|
||
|
Comment distinguer les nombres
décimaux les plus grands ou les plus petits? Il faut les mettre en tableau et les
comparer, dans l'ordre, selon les dixièmes, centièmes, millièmes, etc. Comparez 0,002
/ 1,002 / 0,012 / 0,100 / 0,102 / 0,111 / 0,101 Voir Tableau >>> Attention aux nombres
négatifs –
5,2 < – 3,987654 < – 3,97 < – 0,1 < 0 |
Mise en tableau et en
ordre
|
|
|
|
||
|
Manipulation des
nombres décimaux Pour savoir une fois pour
toutes pourquoi on décale vers la droite ou vers la gauche, voir ce tableau. Voir
Multiplication / Division / Formation
des nombres |
|
|
|
|
|
|
|
|
|
|
|
|
Les anglo-saxons notent les "nombres à virgule"
avec un point à la place de notre virgule
(3,56 devient 3.56). Si le premier chiffre est un zéro, il est omis (0,12
devient .12). Voir Application
à un jeu de nombres When we write numbers, the position, or place, of each number is important:
place value. In the number 678. 54:
As we move left, each position is 10 times
bigger. As well, when we move right, from the decimal point, each position is 10 times
smaller: from Units, to Tens (5), to Hundreds (4) ... |
|
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |